文献标识码: A
2. 国网陕西省电力公司电力科学研究院,西安 710100;
3. 中国电力科学研究院有限公司,武汉 430074;
4. 国网安徽省电力有限公司,合肥 230061
2. State Grid Shaanxi Electric Power Research Institute, Xi'an 710100, China;
3. China Electric Power Research Institute, Wuhan 430074, China;
4. State Grid Anhui Electric Power Co., Ltd., Hefei 230061, China
电力建设的跨越式发展对电网的安全运行提出了更高的挑战。电力变压器作为电网中实现电能远距离输送及分配的枢纽设备,广泛分布于能源富集地及人口密集地,其运行可靠性直接关系到整个电力系统的安全与稳定,一旦因故障而损坏,不仅波及范围广,还会造成人员伤亡及重大经济损失[1-2]。美国电力研究协会(Electric Power Research Institution, EPRI)建立的变压器全行业数据库(Industry Database, IDB)从2006年开始收集数据,目前已记录超过20 000台变压器的数据。IDB的统计数据显示,58.18%的变压器故障发生在绕组,而由于抗短路能力不足导致的故障占比最高,为20.47%[3]。国内关于变压器事故的统计情况所反映的结果也趋于与IDB一致:已公布的统计数据显示,我国约40%的变压器事故由绕组故障引起,且主要原因为抗短路能力不足[4]。变压器绕组机械状态的改变会引起振动信号的改变,因此充分研究绕组的振动机理与特性,并建立起有效的振动模型,才可能全面地了解不同机械状态下的绕组振动响应特性,最终有针对性地利用振动信号进行机械状态的检测,并奠定绕组抗短路能力设计及减振降噪的理论基础[5-8]。
McNutt等人从漏磁场的分布特点入手分析了绕组受力[9],认为:高低压绕组之间轴向的磁场使内线圈产生向内的幅向力,使外线圈产生向外的幅向力,并且呈现中间大,两端小的分布特点;在绕组端部漏磁场的幅向分量使线圈承受轴向的压力,并且呈现两端大、中间小的分布特点。McNutt和Hori Y等人先后将饼式绕组线圈的轴向结构简化为质量−弹簧−阻尼数学模型[9-11],张凡等人进一步完善细化该了模型[12]:将同一线圈的导线视为集中的等效质量块,将压板、紧固件、线圈及垫块等绝缘材料的刚度及阻尼分别视为等效的弹簧和粘壶,从而建立起表征绕组轴向振动的离散动力学模型。汲胜昌等人通过谐响应分析的方法分析了绕组整体的振动分布,指出绕组轴向振动加速度呈现出“M”形的分布规律,即绕组1/4和3/4高度处的加速度幅值较大,绕组端部和中部的加速度幅值较小[13]。
交变的电磁力除了引起轴向振动外,还会引起绕组的幅向振动。徐健学等人在研究中将绕组幅向振动简化为用垫块将绕组线匝等分为圆弧拱的面内弯曲振动,且用固定支撑的欧拉伯努利直梁方程表示该圆弧拱单元的振动[14-15]。张凡对局部导线振动特性进行了详尽的研究,得出了垫块间悬空的导线振动除受到整体线圈振动的耦合作用外,也具有独立于线圈整体的振动特点[16]。
目前,绕组振动机理已较为完善,也建立了较为全面的轴向、幅向的振动模型。但是,当诸如弹簧、阻尼等非线性因素变强时,基于线性理论得出的结果误差会越来越大,无法解释多频响应现象。例如对振动与磁场之间的耦合作用(简称机电耦合)缺乏研究,导致某些变压器振动信号中奇次谐波成分,如50 Hz、150 Hz等,得不到充分的解释。理论上,绕组线圈的受力不仅与漏磁场大小有关,也与线圈间距有关,而在绕组振动的情况下,不断变化的线圈间距会影响线圈所受电磁力,而电磁力又反过来影响绕组振动,因此有必要对绕组受力与振动的关联关系进行整体分析。
为此,本文建立了考虑磁场–振动耦合的变压器绕组振动数学模型,通过理论分析及试验验证确定了绕组多倍频振动产生的条件,从考虑机电耦合的角度完善了绕组振动机理。
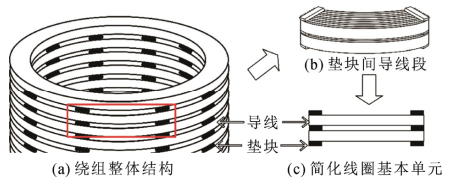
1 两体振动模型 1.1 绕组线圈基本单元绕组是电力变压器的电路部分,一般由连续的绝缘扁导线或圆导线绕制而成,如图 1(a)所示。绕组的基本构成单元为线圈,一般都绕成圆形线匝,再按一定规律的排列和联结。不同电压等级、不同容量的变压器绕组有不同的绕制方法,通常分为层式和饼式2种[17],为了达到电、热、力这3方面的基本要求,线圈之间又由均匀分布的绝缘垫块分隔,如图 1(b)所示,用于增强电气绝缘,利于流动散热,稳定支撑结构。在绕组振动研究中,常见的质量–弹簧–阻尼模型大多针对饼式绕组,因此缺乏普适性。为了全面考虑绕组的非线性振动机理,需要抽象出一个同时具备机械特性及电磁场特性,且具有代表性的基本物理单元。本文将垫块间的导线段作为基本物理单元,如图 1(c)所示,称为简化线圈基本单元。由垫块的作用模式作区别,基本单元存在两种情况,即轴向两体模型及径向两体模型,轴向模型中垫块的作用为提供拉压刚度,径向模型中垫块作用为接触刚度,两者统称为绕组两体模型。
|
图 1 绕组线圈基本单元 Fig. 1 A basic unit of winding coil |
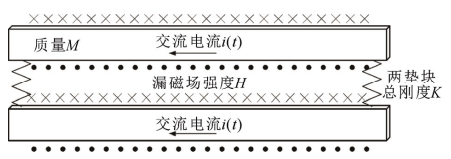
任意两根相邻的导线间都存在电感,导线中流过同向等大的电流,具有同样的物理参数。两体模型为弧长2πr/n的圆弧拱结构,其中r为线圈半径,n为垫块数量。为了满足轴向、幅向稳定性,大型电力变压器绕组圆周分布垫块数 > 12,垫块间的圆心角 < 30°[17],其跨高比 > 15,此时圆弧拱可以近似等效为直梁。因此两体模型可简化如图 2所示,其中有体现机械特性的参数如导线段总质量M以及垫块总刚度K,也有体现电气特性的参数如交流电流i(t)以及漏磁场强度H。下面将对基本两体模型进行分析,建立基于哈密顿原理的两体振动数学模型。
|
图 2 两体物理模型 Fig. 2 The two-wire physical model |
对于两体模型,按照传统分析绕组振动模型时的方法,会固定某一导线作为坐标原点,然而坐标原点的导线事实上也在做着加速运动,如此一来,该参考系并非牛顿力学所适用的惯性参考系。因此,传统的绕组动力学模型存在考虑不全面的地方。哈密顿原理用一个基本假设将全部力学理论进行了统一,主要着眼于整体和能量,由于其表述与坐标选择无关,因此可以处理除牛顿力学以外的非完整、非保守系统,诸如弹性场、电磁场等问题[18]。基于该原理,当同时给定系统的广义坐标和速度后,就可以唯一确定该系统的状态,而且可以预测未来的运动。任意n个可以确定n自由度系统位置的变量s1, s2, s3, …, sn称为该系统的广义坐标,它的导数称为广义速度,二次导数称为广义加速度,加速度与坐标、速度的关系式称为运动方程。根据哈密顿原理,任何一个力学系统都可以用一个相应的函数表征,称为拉格朗日函数:
| $L = L({s_1}, {s_2}, \cdots {s_n}, {\dot s_1}, {\dot s_2}, \cdots {\dot s_n}, t)$ | (1) |
式中:t为时间,该函数满足力学拉格朗日方程
| $\frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial \dot s}} - \frac{{\partial L}}{{\partial s}} = 0$ | (2) |
由于图 2中的两体物理模型与实际变压器绕组有一定区别,为了使问题简化,对该两体模型做出以下基本假设:
1)时变电磁场中,电场和磁场不仅随空间坐标的变化而变化,亦与时间有关。两者不独立,变化的电场产生磁场,变化的磁场产生电场。本文中的两体模型为等位体,位移电流密度远小于传导电流密度,因此可忽略电场力。
2)两体模型中的势能仅仅依赖于所有质点在相同时刻的分布,只要其中一个质点位置发生变化则立即影响其他质点,相互作用为瞬间扩散,即绝对时间假设。
3)电网电流频率为50 Hz,铜材透入深度为9.4 mm,与模型尺寸相近,因此可以忽略交变电流流过导线时在导线中产生的电流趋向于导线表面流动的集肤效应。同时,由于频率较低,影响不明显,因此可以忽略两根导线相互影响产生的邻近效应。
4)变压器油作为振动传递的媒质之一,对振动有一定影响。由于变压器油的粘性,振动的一部分机械能将不可逆地转化为热能,并使振动变得复杂。本模型中,由于变压器油运动黏度低(< 10−5),
且绕组振动频率低(≤1 000 Hz),因此可将变压器油视作理想流体,即不可压缩、不计粘性、无热传导。值得注意的是,虽然在建模过程中忽略油的粘性,但在实际系统中自由振动及共振的能量仍然会被变压器阻尼耗散。
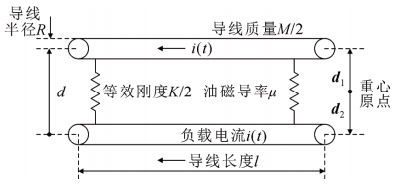
基于以上基本假设条件,利用哈密顿原理及拉格朗日方程构建两体振动数学模型。对如图 3所示的振动模型进行分析。2根导线具有相同方向的相同电流i(t),其长度为l、间距为d、半径为R、质量分别为M/2,μ为变压器油磁导率。由于质点系的内力不能影响它的质心的运动,因此将质心设为原点。上下导线位移分别为向量d1和向量d2,导线间相对位移为dr=d1–d2,d=|dr|。则图 3中模型的电感为
| ${L_{{\rm{all}}}} = \frac{{\mu l}}{{\rm{ \mathsf{ π} }}}{\rm{(}}\ln \frac{d}{R}{\rm{ + }}\frac{1}{4}{\rm{)}}$ | (3) |
|
图 3 两体数学模型示意图 Fig. 3 Schematic diagram of the two-wire mathematical model |
两体模型关于机械能的拉格朗日函数L1为
| ${L_1} = \frac{1}{2}M{\dot d^2} - {E_{\rm{p}}}(d)$ | (4) |
式中,Ep(d)为机械势能,
| ${L_2} = \frac{1}{2}{L_{{\rm{all}}}}{i^2}(t)$ | (5) |
设d0为双导线系统的平衡位置,即无电流时导线的间距。在稳定平衡位置附近的运动是力学系统的一种非常普遍的运动类型,称之为微振动[19]。将弹性势能函数Ep(d)在d0处按幂级数展开,则有
| $\begin{gathered} {E_{\rm{p}}}(d) = {E_{\rm{p}}}({d_0}) + {\left. {\frac{{\partial {E_{\rm{p}}}}}{{\partial d}}} \right|_{d = {d_0}}}(d - {d_0}) + \\ {\left. {\frac{1}{2}\frac{{{\partial ^2}{E_{\rm{p}}}}}{{{\partial ^2}d}}} \right|_{d = {d_0}}}{(d - {d_0})^2}{\rm{ + }} \cdots \\ \end{gathered} $ | (6) |
由于双导线振动时偏离平衡位置很小,因此保留到第一个非零项。零势能点可任意选取,取平衡位置为势能零点,即Ep(d0)=0,则有
| ${E_{\rm{p}}}(d) = K{(d - {d_0})^2}$ | (7) |
采用上述相同的方法,将双导线的磁势能在d0处展开至2阶项。这样,弹性势能与磁势能具有相同的阶数。可得
| $\frac{1}{2}{L_{{\rm{all}}}}{i^2}(t) = \frac{{\mu l}}{{2{\rm{ \mathsf{ π} }}}}{i^2}(t)\left( {\ln \frac{{{d_0}}}{R}{\rm{ + }}\frac{1}{4} + \frac{{d - {d_0}}}{{{d_0}}} - \frac{{{{\left( {d - {d_0}} \right)}^2}}}{{2{d_0}^2}}} \right)$ | (8) |
根据拉格朗日函数的可加性可以得到两体模型整体的拉格朗日函数为
| $\begin{array}{l} L = {L_1} + {L_2} = \\ \quad \quad \frac{1}{2}M{{\dot d}^2} - {E_{\rm{p}}}(d) + \frac{1}{2}L{i^2}(t) = \\ \quad \quad \frac{1}{2}M{{\dot d}^2} - \frac{1}{2}K{(d - {d_0})^2} + \\ \quad \quad \frac{{\mu l}}{{2{\rm{\pi }}}}{i^2}(t)\left( {\ln \frac{{{d_0}}}{R}{\rm{ + }}\frac{1}{4} + \frac{{d - {d_0}}}{{{d_0}}} - \frac{{{{\left( {d - {d_0}} \right)}^2}}}{{2{d_0}^2}}} \right) \end{array} $ | (9) |
将式代入式(9)中,并设x=d–d0(即导线间距相对于平衡位置的偏移量),可得两体模型运动方程为
| $M{\kern 1pt} \ddot x + Kx - \frac{{\mu l}}{{2{\rm{ \mathsf{ π} }}{d_0}}}{i^2}(t) + \frac{{\mu l}}{{2{\rm{ \mathsf{ π} }}d_0^2}}{i^2}(t)x = 0$ | (10) |
式中
对于两体模型的运动方程即式(10),一般情况无法得到其显式解,因此将该方程逐步简化分析,从而得到模型振动特性。
首先对两体模型的基频振动进行分析,以此为基础,进而分析得到考虑耦合因素对振动特性的影响。这类线性系统也称为原非线性系统的派生系统,解称为派生解。假设流经绕组的电流为i(t)=Icosωt,I为电流幅值,ω为电源的角频率,则派生系统振动方程可表示为
| $M{\kern 1pt} \ddot x{\rm{ + }}Kx = \frac{{\mu l{I^2}}}{{2{\rm{ \mathsf{ π} }}{d_0}}}\left( {1 + \cos 2\omega t} \right)$ | (11) |
振动方程的物理实质是力的平衡,式(11)中等号右边为静态情况下导线之间相互作用的电磁力,左边的两项分别为系统的惯性力与弹性力,这类可变外力场作用下的系统振动称为强迫振动。非齐次常系数线性微分方程的通解为齐次方程(自由振动)的通解和非齐次方程(强迫振动)的特解。但由于实际中存在阻尼,自由振动会最终耗散,因此本文中只关注振动方程的稳态解,即:
| $x = \frac{{\mu l{I^2}}}{{2{\rm{ \mathsf{ π} }}{d_0}K}}{\rm{ + }}\frac{{\mu l{I^2}}}{{2{\rm{ \mathsf{ π} }}{d_0}}}\frac{{\cos (2\omega t)}}{{(K - 4{\omega ^2}M)}}$ | (12) |
式中:除去第一项由于恒定力产生的恒定位移分量,绕组线圈振动的角频率为2ω,同静态下磁场力频率相等,为加载电流频率的2倍,这与传统的绕组振动模型的结果一致。对于50 Hz电网系统来说,100 Hz是变压器绕组的基频振动。除此之外,当固有频率为电流频率的2倍时,即
| $x = \frac{{\mu l{I^2}}}{{2{\rm{ \mathsf{ π} }}{d_0}K}}{\rm{ + }}\frac{{\mu l{I^2}}}{{4{\rm{ \mathsf{ π} }}{d_0}}}t\sin (2\omega t)$ | (13) |
可以发现共振使振幅随时间线性增大,直到振动不再是小量。因此在变压器绕组设计时,一定要使固有频率远离激励力频率。
2.2 机电耦合作用下的参变振动特性在绕组线圈振动的情况下,线圈之间的距离会发生周期性的变化,这会导致导线产生的磁场不仅随电流周期变化而变化,还会有自身周期振动带来的影响,即机电耦合作用。存在机电耦合的两体模型振动方程为
| $M{\kern 1pt} \ddot x{\rm{ + }}Kx{\rm{ + }}\frac{{\mu l{I^2}}}{{2\pi {d_0}^2}}\left( {1 + \cos 2\omega t} \right)x = \frac{{\mu l{I^2}}}{{2\pi {r_0}}}\left( {1 + \cos 2\omega t} \right)$ | (14) |
为使方程简化,设y=x−r0,并对式(14)做无量纲化处理,将方程中的各个物理变量表示为关于模型中相应物理常量的相对值。设
| $\frac{{{\rm{d}}{y^2}}}{{{{\rm{d}}^2}\tau }} + \left( {\eta + \lambda (1 + \cos 2\tau )} \right)y = \zeta $ | (15) |
式(15)属于变系数非齐次线性微分方程,表征的是带外激励的参变振动,一般情况下,无法得到方程的显式解。对此,本文对其齐次方程进行近似求解得到其通解,而对于由非齐次项引入的特解,因为非齐次项ζ是τ0的多项式(即常数项或0次多项式),所以特解为常数,为恒定位移,对振动频率无影响。令ε=η+λ,则有
| $\frac{{{\rm{d}}{y^2}}}{{{{\rm{d}}^2}\tau }} + \left( {\varepsilon + \lambda \cos 2\tau } \right)y = 0$ | (16) |
式(16)为马蒂厄方程,本文采用林兹泰德-庞加莱参数摄动法求解其周期解。Krylov和Bogoliubov曾证明若参变项是关于t的周期函数,则对于小扰动λ,系统仍然有同样周期的解,而且存在参数激励频率的1/2解,也称1/2亚谐共振分叉解[20]。因此,λ=0时,为保证线性保守系统有周期等于π或2π的周期解,必须令ε=n2,n=0, 1, 2, …,分别对应于线性无关的特解sin(nτ)和cos(nτ)。除n=0时的周期解为常值解以外,n为偶数时周期为π,n为奇数时周期为2π。将方程式(16)的解y(t)和参数ε都展开成λ的幂级数
| $y(\tau ) = {y_0}(\tau ) + \lambda {y_1}(\tau ) + {\lambda ^2}{y_2}(\tau ) + \cdots $ | (17) |
| $\varepsilon = {\varepsilon _0} + \lambda {\varepsilon _1} + {\lambda ^2}{\varepsilon _2} + \cdots $ | (18) |
式中
将式(17)及式(18)带入方程(16),令两边λ的同次幂项系数相等,导出各阶近似的线性方程组为
| $\left\{ \begin{array}{l} {\lambda ^0}{{\ddot y}_0} + {n^2}{y_0} = 0\\ {\lambda ^1}{{\ddot y}_1} + {n^2}{y_1} + {\varepsilon _1}{y_0} + {y_0}\cos 2\tau = 0\\ {\lambda ^2}{{\ddot y}_2} + {n^2}{y_2} + {\varepsilon _2}{y_0} + {\varepsilon _1}{y_1} + {y_1}\cos 2\tau = 0\\ \; \vdots \end{array} \right.$ | (19) |
下面分别讨论n不同值时的情况:
1)n=0时,则有
| ${\ddot y_1} + {\varepsilon _1} + \cos 2\tau = 0$ | (20) |
根据消除长期项的条件,ε1必须为零,从而得到周期解
| ${y_1} = \frac{1}{4}\cos 2\tau $ | (21) |
再进一步代入式(19)中的λ2对应的方程可得
| ${\ddot y_2} + {\varepsilon _2} + \frac{1}{8} + \frac{1}{8}\cos 4\tau = 0$ | (22) |
同样根据消除长期项的条件,ε2=-1/8,从而得到周期解
| ${y_2} = \frac{1}{{128}}\cos 4\tau $ | (23) |
如此继续计算下去即可得到满足精度的解
| $y = 1{\rm{ + }}\frac{\lambda }{4}\cos 2\tau {\rm{ + }}\frac{{{\lambda ^2}}}{{128}}\cos 4\tau {\rm{ + }} \cdots $ | (24) |
2)n=1时,则有ε=η+λ≈η=1,也即系统固有频率与电源频率相近时,此时y0有2个线性无关的特解即cosτ和sinτ。首先采用y0=cosτ,则可得
| $ \left\{ \begin{array}{l} {\varepsilon _0}{\rm{ = 1}},{y_0} = \cos \tau \\ {\varepsilon _1} = - \frac{1}{2},{y_1} = \frac{1}{{16}}\cos 3\tau \\ {\varepsilon _2} = - \frac{1}{{32}},{y_2} = - \frac{1}{{256}}\cos 3\tau {\rm{ + }}\frac{1}{{768}}\cos 5\tau \\ \; \vdots \end{array} \right.$ | (25) |
同样的,利用y0=sinτ,可得
| $ \left\{ \begin{array}{l} {\varepsilon _0}{\rm{ = 1}},{y_0} = \sin\tau \\ {\varepsilon _1} = \frac{1}{2},{y_1} = \frac{1}{{16}} \sin3\tau \\ {\varepsilon _2} = - \frac{1}{{32}},{y_2} = \frac{1}{{256}} \sin3\tau {\rm{ + }}\frac{1}{{768}} \sin5\tau \\ \; \vdots \end{array} \right.$ | (26) |
3)n=2时,则有ε=η+λ≈η=4,也即系统固有频率为电源频率的2倍时,此时y0有两个线性无关的特解即cos2τ和sin2τ。首先采用y0=cos2τ,则可得
| $\left\{ \begin{array}{l} {\varepsilon _0} = 4,{y_0} = \cos 2\tau \\ {\varepsilon _1} = 0,{y_1} = - \frac{1}{8} + \frac{1}{{24}}\cos 4\tau \\ {\varepsilon _2} = \frac{5}{{48}},{y_2} = \frac{1}{{1536}}\cos 6\tau \\ \; \vdots \end{array} \right.$ | (27) |
同样的,利用y0=sin2τ,可得
| $ \left\{ \begin{array}{l} {\varepsilon _0}{\rm{ = }}4,{y_0} = \sin 2\tau \\ {\varepsilon _1}{\rm{ = }}0,{y_1} = \frac{1}{{24}}\sin 4\tau \\ {\varepsilon _2} = - \frac{1}{{48}},{y_2} = \frac{1}{{1536}}\sin 6\tau \\ \; \vdots \end{array} \right.$ | (28) |
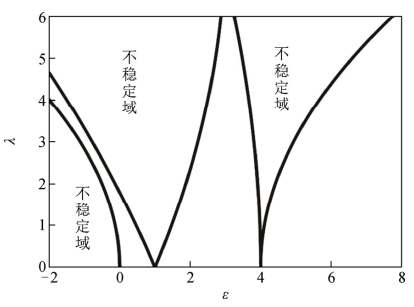
如此继续计算直到满足精度要求时为止。系统在参数激励下所产生的响应可能微弱,也可能剧烈共振,这取决于参变系统的稳定性。两体模型参变系统存在稳定域和不稳定域,取决于参数λ和ε。根据上述λ和ε推导的关系式称为边界曲线或者转迁曲线,它们将平面(λ,ε)分割成稳定区域和不稳定区域,如图 4所示为参变共振稳定图。其中当ε=n2,n=0, 1, 2, …时,线性系统即使受到微弱的参数激励,也可以产生剧烈的参数共振。
|
图 4 两体模型参变振动稳定图 Fig. 4 Stable region of parametric vibration of the two-wire model |
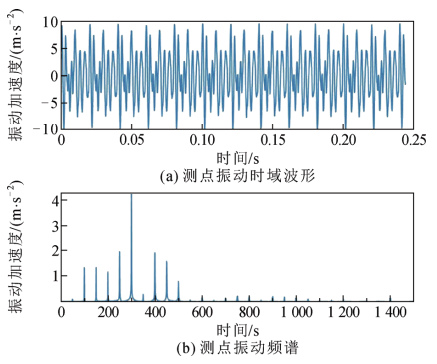
由以上分析可得,当变压器绕组的固有频率,激励频率满足一定的条件时,会产生参数共振,具体表现为:当系统固有频率与电源频率相近时,出现激励电流的奇次倍频率(2n-1)ω,当系统固有频率为电源频率2倍时,出现偶次倍频率2nω,n=1, 2, …。不过频率越高,幅值越小,甚至可以忽略不计,在50 Hz电网系统中,将主要存在一倍频(50 Hz),基频(100 Hz),四倍频(200 Hz)等频率。这是稳定运行状态下,绕组振动区别于铁芯的明显特征之一。以往研究中在无直流偏磁的情况下,常将奇次谐波振动当作测量系统的空间电磁耦合干扰忽略掉,然而这样就丢掉了绕组重要的机械状态信息。因此在后续的振动信号分析过程中,需要全面考虑所有振动信号才能得到准确的设备信息。在大量的试验过程中发现:绕组越松动、电压等级越大、容量越大的变压器,出现奇次谐波的情况越多,如图 5所示为某500 kV变压器在线振动信号,其中存在大量奇次谐波。这是因为这些情况下绕组固有频率较低,更容易满足上述参变共振的条件。
|
图 5 某500 kV电力变压器油箱在线振动信号 Fig. 5 On-line vibration signal of the oil tank of a 500 kV power transformer |
对上述两体模型的多倍频机理进行试验验证,首先对实际变压器绕组进行试验模态分析,从而得到固有频率等模态参数;然后对绕组施加扫频激励,观察当激励频率与固有频率在满足上述特定条件时,其振动信号是否出现理论分析中的多倍频现象。
3.1 绕组试验模态分析使用一台0.4/10 kV,50 kVA的单相饼式线圈双绕组模型变压器进行试验验证,试验时将变压器本体放置于油箱中。选择最为简单且最常用的SISO(单点激励,多点输出)参数识别技术,一次测试只激励一个点的一个方向。本文选择紧邻垫块的压板螺钉作为激励点,垂直方向为激励方向。为获取整体绕组的模态特征,在绕组上纵向平均选择7个拾振点测量绕组线饼的轴向振动,测点紧邻垫块位置,由压钉传递过来的力经过压板、垫块、线饼到达拾振点,越接近连接处,能量衰减越小,从而使结构的响应有较高的信噪比。测量系统由压电式振动加速度传感器PCB352C65、模态调谐ICP力锤PCB086C03、多通道同步数字采集卡NI9234,模态分析软件及硬件构成,可实现信号的同步预触发采集以及实时分析功能,传感器具体参数分别如表 1所示,采集卡采样频率为10 240 Hz。
|
|
表 1 传感器参数 Table 1 Parameters of the sensors |
在获得所有测点的频响函数(FRF)后,通过如下方式求取整体绕组的模态参数[21]:
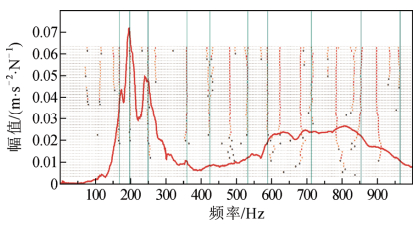
1)使用求和函数(SUM)对所有测点的FRF进行求和,使得绕组在模态频率处达到极值,如图 6所示为模型变压器绕组频响曲线,可以发现,由于阻尼的存在,共振峰较为平缓,且高频愈加明显。频响函数在150 Hz以下的频段很少有共振峰。
|
图 6 频响函数曲线 Fig. 6 Frequency response function curve |
2)采用最小二乘复频域法(PolyMAX)对上步所得的总和FRF进行模态参数识别,初步确定绕组的模态参数。该方法对模态重叠较严重的系统,或者频响函数数据存在噪声污染情况,都能给出比较准确的稳态图,可以灵活地识别高密度密集模态。
3)采用模态置信准则(MAC),来评价2个模态振型向量几何上的相关性,值为0~1之间。越接近于0,说明两个振型相关性越小,振型越独立。由于绕组模态参数主要用于扫频激励下绕组振动特性的验证,因此对振型正交的要求较小,本文设定满足MAC矩阵对角线元素值< 0.4这一条件时,基本可以认为振型向量相互独立,可以确定固有频率等模态参数。
由于变压器在正常工作中振动主要集中在1 000 Hz以下,因此本文仅针对1 000 Hz以内的模态参数进行分析。基于以上步骤和方法,求得绕组前10阶模态参数如表 2所示,固有频率都 > 150 Hz。根据2.2节中所提的参变共振条件可知:正常情况下,该绕组振动信号将主要存在100 Hz振动。
|
|
表 2 绕组模态参数 Table 2 Winding modal parameters |
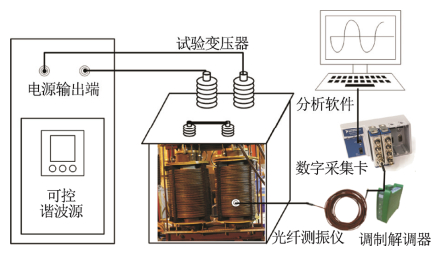
变压器绕组的结构、材料等参数一旦设计好,其模态参数便同时确定,要通过改变设计好的绕组结构获得想要的模态参数十分困难。为了验证绕组的多倍频振动现象,本文设计了通过改变激励电流频率来满足绕组多倍频振动条件的试验平台以及相应的测量系统,如图 7所示。试验平台主要包括可控谐波源及试验变压器。通过可控谐波源为绕组提供激励电流,其额定容量为180 kVA,输出频率范围为50~2 500 Hz,每个频率分量的幅值和相位连续可调。在带电试验中,为了满足绝缘要求保证安全,防止接触式传感器与绕组发生短路导致试验人员触电以及测试系统损坏,绕组上布置光纤加速度传感器EVA1106A,油箱上布置振动加速度传感器PCB352C65,参数如表 1所示。
|
图 7 实验回路及测量系统 Fig. 7 Experimental circuit and measurement system |
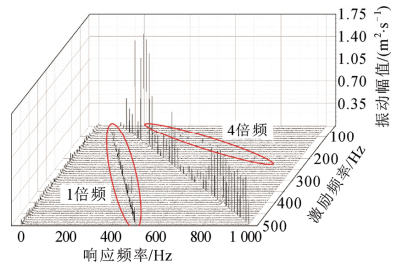
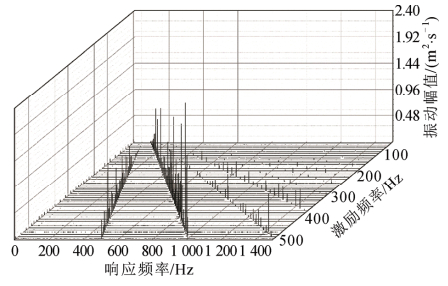
试验中由于二次侧短路,因此绕组两端电压很小,励磁电流很小,因此铁芯几乎不产生磁致伸缩振动,在绕组上测得的振动信号主要为通流线圈在漏磁场中的振动导致的。对绕组施加不同频率的正弦电流,并保持电流大小统一为100 A。扫频试验起始频率为50 Hz,步长10 Hz,直至500 Hz。根据2.2节理论推导的振动特性,主要关注绕组的1倍频响应(即1倍电流频率)、2倍频响应(即2倍电流频率)、4倍频响应(即4倍电流频率)。图 8、图 9分别为绕组和变压器油箱上的扫频激励响应。
|
图 8 绕组扫频激励振动响应 Fig. 8 Sweep frequency excitation vibration response of winding |
|
图 9 变压器油箱扫频激励振动响应 Fig. 9 Sweep frequency excitation vibration response of oil-tank |
扫频电流激励下,图 8所示的绕组的振动主要成分为2倍频响应。另外结合表 2中的模态参数可得,在满足固有频率与电流激励频率相近的条件下,出现了1倍频,在固有频率约为电流频率2倍时出现了4倍频,这一现象与前文中的理论分析一致。图 9所示的变压器油箱振动响应比绕组振动响应更加丰富,在1 500 Hz范围内几乎存在所有整数倍频成分,这是由于油箱上的振动信号为绕组振动的汇总,不同位置的线圈有不同的局部模态参数,因此绕组不同位置的导线会在不同频率处满足参变共振条件。另外,在某一频率电流激励下,随着振动响应频率的升高,其幅值有所减小,这与前文的理论分析一致。为了量化以上多倍频现象的程度,提出总谐波畸变率(total harmonics distortion,THD),即波形相对正弦波畸变的程度,来表征参变共振对绕组振动响应的影响,其定义为全部谐波含量均方根值与基波均方根值之比,计算式为
| ${R_{{\rm{THD}}}} = \frac{{\sqrt {\sum\limits_k {{{\left( {A_{{\rm{rms}}}^{(k)}} \right)}^2}} } }}{{A_{{\rm{rms}}}^{(1)}}} \times 100\% $ | (29) |
式中:

|
图 10 扫频激励振动响应总谐波畸变率 Fig. 10 RTHD of sweep frequency excitation vibration response |
工频电力变压器绕组中主要流过50 Hz电流,在正常情况下,绕组结构对称且稳定,固有频率较高,较难满足参变共振条件,因此绕组振动主要为基频100 Hz。但有研究发现,当绕组发生松动或者变形时,整体模态频率大小下降,某些固有频率处出现分叉,造成固有频率数量增多,因此绕组机械状态恶化过程中,将可能出现满足参变共振条件的情况[16, 22]。另外,随着直流系统的发展,电网中往往存在高次谐波,无论是工频变压器,还是换流变压器、中频变压器等特殊变压器以及电抗器等线圈类设备,绕组中都会存在高次谐波,这也使得绕组更容易出现参变共振现象。因此在变压器绕组故障诊断、抗短路能力设计、减振降噪措施研究中,都应该考虑机电耦合带来的参变共振多倍频振动。
4 结论本文根据变压器绕组的结构特点,提出考虑机电耦合的绕组振动模型,并试验验证了该理论模型的准确性。主要结论如下:
1)从线圈中抽象出的两体振动模型兼具机械特性及电磁场特性。采用哈密顿原理对机械系统及电磁系统统一分析,可以得出两体模型的振动数学方程,通常绕组的振动主要集中在基频100 Hz处。
2)在机电耦合作用下,当绕组固有频率满足电流激励的整数倍时,会出现参变共振多倍频振动,振动频率为电流频率的整数倍。
3)试验模态分析及扫频振动响应法可以验证绕组振动中存在机电耦合作用。考虑机电耦合的绕组两体振动模型完善了绕组振动机理,提出相应特征值表征参变共振对绕组振动的影响。
本文主要研究了绕组的振动机理及特性,丰富了变压器故障诊断及减振降噪的理论基础。为提高该理论的工程应用价值,未来还需对各种故障情况下的振动特性及具体减振降噪措施开展研究。
| [1] |
汲胜昌, 师愉航, 张凡, 等. 电力变压器振动与噪声及其控制措施研究现状与展望[J]. 高压电器, 2019, 55(11): 1-17. JI Shengchang, SHI Yuhang, ZHANG Fan, et al. Review on vibration and noise of power transformer and its control measures[J]. High Voltage Apparatus, 2019, 55(11): 1-17. (  0) 0) |
| [2] |
汲胜昌, 张凡, 师愉航, 等. 基于振动信号的电力变压器机械状态诊断方法研究综述[J]. 高电压技术, 2020, 46(1): 257-272. JI Shengchang, ZHANG Fan, SHI Yuhang, et al. Review on vibration-based mechanical condition monitoring in power transformers[J]. High Voltage Engineering, 2020, 46(1): 257-272. (  0) 0) |
| [3] |
Working Group A2.37. Transformer reliability survey[R]. Paris, France: CIGRE, 2015.
(  0) 0) |
| [4] |
王梦云. 2005年度110(66)kV及以上变压器事故与缺陷统计分析[J]. 电力设备, 2006, 7(11): 99-102. WANG Mengyun. Statistics and analysis of the faults and defects of 110(66)kV and the above transformers in 2005[J]. Electrical Equipment, 2006, 7(11): 99-102. (  0) 0) |
| [5] |
朱叶叶, 汲胜昌, 张凡, 等. 电力变压器振动产生机理及影响因素研究[J]. 西安交通大学学报, 2015, 49(6): 115-125. ZHU Yeye, JI Shengchang, ZHANG Fan, et al. Vibration mechanism and influence factors in power transformers[J]. Journal of Xi'an Jiaotong University, 2015, 49(6): 115-125. (  0) 0) |
| [6] |
王峰, 王春宁. 基于辨识模型的变压器故障诊断方法研究[J]. 江苏电机工程, 2014, 33(1): 26-29. WANG Feng, WANG Chunning. Research on transformer fault detection based on identification model[J]. Jiangsu Electrical Engineering, 2014, 33(1): 26-29. (  0) 0) |
| [7] |
谢坡岸, 金之俭, 饶柱石, 等. 振动法检测空载变压器绕组的压紧状态[J]. 高电压技术, 2007, 33(3): 188-189. XIE Po'an, JIN Zhijian, RAO Zhushi, et al. Detection on winding clamping pressure in power transformers through vibration analysis[J]. High Voltage Engineering, 2007, 33(3): 188-189. DOI:10.3969/j.issn.1003-6520.2007.03.048 (  0) 0) |
| [8] |
张彬, 徐建源, 陈江波, 等. 基于电力变压器振动信息的绕组形变诊断方法[J]. 高电压技术, 2015, 41(7): 2341-2349. ZHANG Bin, XU Jianyuan, CHEN Jiangbo, et al. Diagnosis method of winding deformation based on power transformer vibration information[J]. High Voltage Engineering, 2015, 41(7): 2341-2349. (  0) 0) |
| [9] |
MCNUTT W, JOHNSON W, NELSON R, et al. Power transformer short-circuit strength - requirements, design, and demonstration[J]. IEEE Transactions on Power Apparatus and Systems, 1970, PAS-89(8): 1955-1969. DOI:10.1109/TPAS.1970.292780 (  0) 0) |
| [10] |
HORI Y, OKUYAMA K. Axial vibration analysis of transformer windings under short circuit conditions[J]. IEEE Transactions on Power Apparatus and Systems, 1980, PAS-99(2): 443-451. DOI:10.1109/TPAS.1980.319680 (  0) 0) |
| [11] |
TAMAKI E, KISHI A, ITOH S, et al. The coil mechanical behavior under short circuit[C]//CIGRE Transformer Colloquium 1999 in Budapest. Budapest, Hungary: CIGRE, 1999: 1386- 1391.
(  0) 0) |
| [12] |
ZHANG F, JI S, MA H. Operational modal analysis of transformer windings[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1285-1298. DOI:10.1109/TPWRD.2019.2939388 (  0) 0) |
| [13] |
汲胜昌, 张凡, 钱国超, 等. 稳态条件下变压器绕组轴向振动特性及其影响因素[J]. 高电压技术, 2016, 42(10): 3178-3187. JI Shengchang, ZHANG Fan, QIAN Guochao, et al. Characteristics and influence factors of winding axial vibration of power transformer in steady-state operation condition[J]. High Voltage Engineering, 2016, 42(10): 3178-3187. (  0) 0) |
| [14] |
徐健学, 黄洪, 张培真, 等. 弹性支持扁拱动力稳定性分析和变压器内线圈短路动稳定分析[J]. 应用力学学报, 1992(2): 14-25. XU Jianxue, HUANG Hong, ZHANG Peizhen, et al. Dynamic stability of shallow arch with elastic supports -application to the dynamic stability analysis of inner windings of transformer during short-circuit[J]. Chinese Journal of Applied Mechanics, 1992(2): 14-25. (  0) 0) |
| [15] |
张凡, 汲胜昌, 师愉航, 等. 电力变压器绕组振动及传播特性研究[J]. 中国电机工程学报, 2018, 38(9): 2790-2798. ZHANG Fan, JI Shengchang, SHI Yuhang, et al. Research on transformer winding vibration and propagation characteristics[J]. Proceedings of the CSEE, 2018, 38(9): 2790-2798. (  0) 0) |
| [16] |
张凡. 电力变压器绕组振动特性及其机械状态检测方法研究[D]. 西安: 西安交通大学, 2019. ZHANG Fan. Research on vibration characteristics of power transformer windings and its mechanical condition monitoring[D]. Xi'an, China: Xi'an Jiaotong University, 2019: 62-73. (  0) 0) |
| [17] |
赵静月. 变压器制造工艺[M]. 北京: 中国电力出版社, 2009. ZHAO Jingyue. Transformer manufacturing process[M]. Beijing, China: China Electric Power Press, 2009. (  0) 0) |
| [18] |
梁昆淼. 力学: 理论力学[M]. 北京: 高等教育出版社, 2009: 80-97. LIANG Kunmiao. Mechanics: theoretical mechanics[M]. Beijing, China: Higher Education Press, 2009: 80-97. (  0) 0) |
| [19] |
朗道, 栗费席兹. 理论物理学教程[M]. 李俊峰, 译. 第5版. 北京: 高等教育出版社, 2007: 2-4, 83-87. LANDAU L D, LIFSHITZ E M. Course of theoretical physics[M]. LI Junfeng translated. 5th edition. Beijing, China: Higher Education Press, 2007: 2-4, 83-87. (  0) 0) |
| [20] |
张伟. 非线性动力学理论与应用的新进展[M]. 北京: 科学出版社, 2009. ZHANG Wei. New development of nonlinear dynamics theory and application[M]. Beijing, China: Science Press, 2009. (  0) 0) |
| [21] |
谭祥军. 从这里学NVH[M]. 北京: 机械工业出版社, 2018: 294-306. TAN Xiangjun. Learn NVH from here[M]. Beijing, China: Machinery Industry Press, 2018: 294-306. (  0) 0) |
| [22] |
许洪华, 陈冰冰, 弓杰伟, 等. 基于有限元模型的变压器绕组松动研究[J]. 电力工程技术, 2016, 35(2): 23-25. XU Honghua, CHEN Bingbing, GONG Jiewei, et al. Research on transformer winding looseness based on finite element model[J]. Electric Power Engineering Technology, 2016, 35(2): 23-25. DOI:10.3969/j.issn.1009-0665.2016.02.006 (  0) 0) |




