徐志钮1979—,男,博士,副教授,硕导,主要从事光纤分布式传感技术及在电气设备状态检测及故障中的应用等方面的研究E-mail: wzcnjxx@sohu.com
0 引言
光纤传感(optical fiber sensing, OFS)是自20世纪70年代发展起来的传感技术。与传统传感技术相比,光纤传感具有质量轻、体积小、抗电磁干扰能力强、安全性高、耐高温、便于融合进物联网等优点[1-2],在特殊环境下可完成传统传感器无法实现的任务,近些年在电气设备状态监测领域逐渐得到应用[3-7]。
光纤传感按原理基本可分为单点光纤传感[8]、准分布光纤传感[9]和全分布光纤传感[10-11]3类。基于布拉格光栅的光纤光栅传感和干涉型光纤传感器属于单点光纤传感技术,其仅可在极小范围内监测选定点附近的参量变化;在单点传感基础上,Ren L将光纤光栅传感技术的传感点连接成1条离散的传感路径,实现了准分布式光纤传感[12]。但该技术只能监测预先设置传感单元位置的状态,并非真正的全分布式传感,且随着传感单元设置数量的增加其成本、施工难度等会显著上升;随着技术的发展,全分布式光纤传感技术逐渐成熟,该类技术除具有传统光纤传感的优点外,还可实现长距离、大范围的传感[13],1根光纤即可代替成千上万个点式传感器,具有很好的应用前景。
目前主要有基于瑞利散射、拉曼散射和布里渊散射的3类分布式光纤传感技术[14]。基于瑞利散射的光时域反射技术(optical time domain reflectometer, OTDR)常用于光纤断点和损耗监测,其对温度和应变不敏感,测量精度较低,且较难实现长距离的监测。基于拉曼散射的光纤传感技术可实现沿线温度的监测,但其无法监测应力且测量范围通常小于30 km,难以实现更长距离监测[15]。基于布里渊散射的分布式光纤传感技术可实现温度和应变的监测,且具有长监测距离、高空间分辨率和高测量精度的特点,其性能明显优于前2种技术[16],在电气设备的监测中具有良好的应用前景。应用布里渊光时域反射(Brillouin optical time domain reflectometer, BOTDR)技术有实现光纤复合海底电缆的应变和温度监测的报道[17-18];基于布里渊光时域反射技术和光纤光栅(fiber Bragg grating, FBG)技术相结合可实现分布式在线温度和应变光纤传感系统[19],基于该系统可实现100 km以内架空输电线路温度的在线监测。
通常来说,基于布里渊散射的传统分布式传感技术采用谱拟合法获得布里渊频移(Brillouin frequency shift, BFS)。谱拟合法为保证测量的精度,扫频点数不会选取的过少,导致测量时间为分钟级[20],甚至更长。虽然通过采用快速布里渊频移提取方法[21-22]可有效减少测量的总耗时,但该方法的实时性仍有待于进一步提高。为减少测量时间,R. Bernini和A. Minardo等在2009年首次提出了基于布里渊散射的单斜坡法(slope-assisted BOTDA, SA-BOTDA)[23],该技术仅需选取1个探测光频率即可解调出布里渊频移,极大缩短了测量时间。2014年,A. Motil提出了基于布里渊分布式光纤传感的双斜坡法(double slope-assisted BOTDA, DSA-BOTDA)[24],该方法通过测量2处探测光频率来解调布里渊频移,一定程度上牺牲了测量速度,但免除了功率波动造成的测量误差。单斜坡法和双斜坡法实现了基于布里渊散射的光纤分布式传感的快速测量,Aldo Minardo在2013年采用单斜坡法实现了铁路的在线动态监测[25];2017年,Damien Maraval将单斜坡法应用于管道振动监测[26]。以上研究显著推动了基于光纤分布式传感的温度和应变快速测量的进步。但该方面尚存在以下问题:1)2种斜坡法以及谱拟合法针对实测布里渊谱的性能比较未见文献公开报道;2)双斜坡法的左右2个工作点以及布里渊谱信噪比对布里渊频移测量准确性的影响未见报道。
本文将谱拟合法、单斜坡法和双斜坡法应用于裸光纤、光纤复合架空地线(optical fiber composite overhead ground wire, OPGW)和光电复合海缆监测,并对效果进行了比较,指出了斜坡法尤其是双斜坡法的特点和优势。在此基础上基于数值产生和实测光纤沿线的布里渊谱研究了左右两侧工作点和布里渊谱信噪比对双斜坡法提取布里渊频移准确性的影响,并确定了最佳工作点。本文工作对基于布里渊散射的分布式光纤温度和应变快速测量技术在输电线路乃至电气设备监测领域的应用具有较好的参考价值。
1 原理介绍
1.1 基于布里渊散射的温度和应变测量
通常来说光纤分布式传感中入射光为矩形光脉冲,布里渊谱近似满足伪Voigt模型,表示如下

式中:
伪Voigt模型不仅能较好逼近Voigt模型,而且避免了卷积的计算,计算量不是很大,编程实现也相对容易。因此,也有大量布里渊频移提取方法是基于以上的伪Voigt模型。
谱峰对应频率称为布里渊频移,光纤温度及应变与布里渊频移呈线性关系,如式(2)所示。
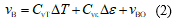
式中:
因此,基于温度和应变敏感系数、基准条件下的布里渊频移以及实测的布里渊频移即可解析光纤中的温度或应变。
1.2 基于谱拟合的频移提取方法
采用非线性最小二乘拟合方法,建立目标函数如下
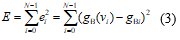
式中:
以上的目标函数采用Levenberg-Marquardt算法优化,对应待优化变量的修正计算式为
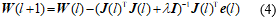
式中
.

当目标函数趋于最小化后,得到最优化的
1.3 基于单斜坡的频移提取方法
不同于谱拟合法的完整扫频,单斜坡法只需在布里渊谱上升或下降斜坡选取1个探测光频率(称为工作点[23],其值为
设
\(\delta {{v}_{\text{B}}}={{v}_{\text{B1}}}-{{v}_{\text{B}0}}\) (6)
式中:
以洛伦兹线型为例,工作点选择为布里渊频移的左侧半峰(

 图1
布里渊谱及参数
Fig.1
Brillouin spectrum and its parameters
图1
布里渊谱及参数
Fig.1
Brillouin spectrum and its parameters
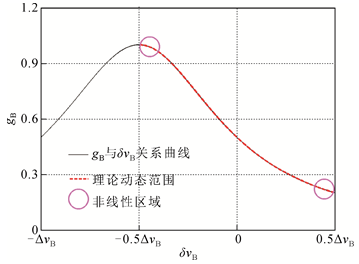
 图2
单斜坡法中
图2
单斜坡法中
虽然布里渊频移处于理论动态范围内时可以采用单斜坡法计算布里渊频移,但非线性区间内灵敏度偏低或由于引入模型的原因会导致更大的误差。因此,其动态范围也比较有限。
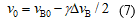
根据基准谱可以确定工作点处增益与布里渊频移的关系,再结合实测条件下工作点处的增益即可获得对应的布里渊频移。研究表明,最佳的
单斜坡法扫频个数为1,极大地缩短了测量时间,优势十分明显。但受制于布里渊谱的线性区域,其动态范围(可应用范围)较小,超出该范围时噪声的影响变大;同时功率波动的影响给探测光频率处测得的增益值带来了一定误差,对其测量准确性产生了一定的影响。
1.4 基于双斜坡的频移提取方法
与单斜坡法不同,双斜坡法通过在基准谱上升与下降斜坡处各选择1个频率点,根据其对应增益比值的对数来解调布里渊频移信息[24],表示为
.
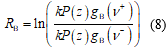
式中:
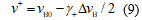
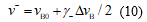
显然
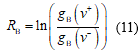
由式(11)可知,双斜坡法通过对光纤2个频移对应的布里渊增益进行比值取对数得到
.选取初始布里渊频移
虽然双斜坡法利用了2个频率点增益的比较抑制了功率波动造成的误差,但比值方式可能会进一步放大增益误差,其与单斜坡相比准确性如何需要系统验证。
布里渊谱测量时间
\({{t}_{\text{T}}}=N({{t}_{\text{sf}}}+{{N}_{\text{at}}}T)\) (12)
式中:
由式(12)可知,谱测量时间与扫频点数成正比,从测量耗时的角度来看,由于谱拟合法需要测量几十个频率点,而单斜坡法和双斜坡法仅分别需要测量1和2个频率点。因此,斜坡法的测量时间可能仅为谱拟合法的几十分之一,这当然与扫频点数有关。由于无需涉及谱拟合,它们的另外一个优势是计算速度很快,一旦谱测量完成,很快就能获得光纤沿线的布里渊频移。
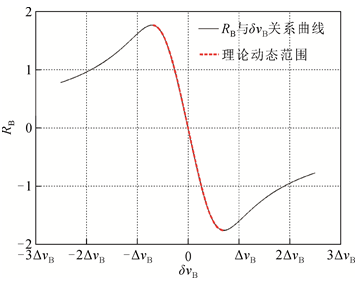
 图3
双斜坡法中
图3
双斜坡法中
2 输电线路监测中的应用
本章采用实测谱比较不同方法的效果。不失一般性,
2.1 裸光纤
由于输电线路中敷设的光纤多为裸光纤,或含有护套的裸光纤。缠绕于光纤轴上的裸光纤也会承受应变,使得布里渊频移随光纤沿线逐渐变化,能较好模拟输电线路中敷设光纤的状况,而且裸光纤长度可以更加灵活选择,可以采集更多的布里渊谱去充分验证结果的可靠性。因此,本节选择其进行分析。待分析的裸光纤为1盘长度为1 km左右的G657A2型单模光纤,采用BOTDR在室温下测量布里渊谱。扫频范围为10.52~10.92 GHz,扫频间隔为1 MHz,量程为2 km,入射脉宽为200 ns,波长为1 550 nm。如果信噪比太低则双斜坡法误差太大,可能不能满足实际要求,如果信噪比很高则要求叠加平均次数很高,测量的实时性受到限制,综合考虑叠加平均次数为212。采用基于伪Voigt模型的谱拟合法得到峰值处的信噪比为32.53 dB。为了获得信噪比较高情况下的光纤沿线布里渊谱作为基准谱,叠加平均次数选择足够高的218,采用基于伪Voigt模型的谱拟合法获得峰值处的信噪比为45.12 dB,线宽和布里渊频移的均值分别为41.08 MHz和10 724.36 MHz。根据式(7)可得单斜坡法工作点选择为10 704 MHz,根据式(9)—式(10)可得双斜坡法工作点分别选择为10 704和10 745 MHz。
选择1个典型基准谱及对应基于伪Voigt模型的谱拟合法结果如
针对叠加平均次数为212的信号,3种方法的布里渊频移计算结果与高信噪比情况(叠加平均次数为218)的比较如
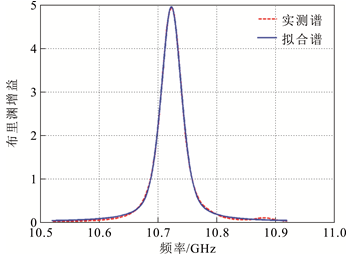
 图4
裸光纤高信噪比的布里渊谱及拟合结果(叠加平均次数为218,入射光脉宽为200 ns)
Fig.4
Measured spectrum with high SNR for bare fiber and corresponding fitted curve(average time is 218, incident light pulse width is 200 ns)
图4
裸光纤高信噪比的布里渊谱及拟合结果(叠加平均次数为218,入射光脉宽为200 ns)
Fig.4
Measured spectrum with high SNR for bare fiber and corresponding fitted curve(average time is 218, incident light pulse width is 200 ns)
坡法的误差为单斜坡法的48.28%。由式(12)可知,测量时间与扫频点数成正比。扫频401个点时光纤沿线20 000个谱的测量时间为541 s,故结合式(12)可知,单斜坡和双斜坡法测量时间仅分别为1.35和2.70 s。斜坡法可有效减少测量时间。
双斜坡法准确性比单斜坡法更高的原因除了其利用2个频率点的信息外,还通过比值消除了不同次测量之间的布里渊增益的波动,而后者对单斜坡法来说几乎无法直接避免。
2.2 光纤复合架空地线
待分析的光纤复合于220 kV的OPGW中,长度约为14 km。实测布里渊谱的扫频范围为10.4~11.2 GHz,扫频间隔为5 MHz。量程为20 km。入射脉宽为20 ns,波长为1 550 nm,叠加平均次数为213。采用基于伪Voigt模型的谱拟合法得到光纤沿线线宽和布里渊频移的均值分别为81.69 MHz和10 830.58 MHz,峰值处布里渊谱的信噪比为30.98 dB。因此,根据式(7)得到单斜坡法工作点选择为10 790 MHz,根据式(9)—式(10)可得双斜坡法工作点分别选择为10 790和10 870 MHz。针对典型的实测谱,采用基于伪Voigt模型谱拟合法的拟合结果如
由

 图5
不同方法算得光纤沿线的布里渊频移(裸光纤)
Fig.5
Brillouin frequency shift along optical fiber estimated by different methods(bare fiber)
图5
不同方法算得光纤沿线的布里渊频移(裸光纤)
Fig.5
Brillouin frequency shift along optical fiber estimated by different methods(bare fiber)
由

 图6
OPGW复合光纤实测谱及对应的拟合结果
Fig.6
Measured spectrum of OPGW composited fiber and corresponding fitted curve
图6
OPGW复合光纤实测谱及对应的拟合结果
Fig.6
Measured spectrum of OPGW composited fiber and corresponding fitted curve

 图7
不同方法算得OPGW复合光纤沿线的布里渊频移
Fig.7
Brillouin frequency shift along optical fiber composited in OPGW estimated by different methods
图7
不同方法算得OPGW复合光纤沿线的布里渊频移
Fig.7
Brillouin frequency shift along optical fiber composited in OPGW estimated by different methods
拟合法的差距分别为2.87和1.02 MHz。考虑到此时谱拟合准确性较高,将谱拟合法得到的布里渊频移作为准确值,则双斜坡法的误差为单斜坡法的35.54%。具体而言单斜坡法在0~3 km左右得到的布里渊频移与谱拟合法结果差距偏大,这是因为单斜坡法线性范围较小,进入了非线性区间,误差增大。
普通单模光纤的温度和应变的敏感系数非常稳定,分别取值为1.06 MHz/℃和0.047 7 MHz/10-6。但针对不同类型和批次的光纤基准温度下的布里渊频移会有一定的波动,由于该光纤已经复合于OPGW中无法取出后测量,故查阅文献后取基准温度下布里渊频移为10.8 GHz(即实际工程应用时在厂家复合光纤之前可实测基准温度下的布里渊频移)。考虑到OPGW沿线的温度近似为同一值,其光纤沿线布里渊频移的变化主要由应变导致,结合式(2)可得3种方法算得的光纤应变如
本案例如果使用谱拟合法,则测量OPGW复合光纤上所有布里渊谱需要的时间为595.75 s。扫频点数为161,故结合式(12)可知,如果采用单斜坡和双斜坡法则对应的测量时间仅分别为3.61和7.22 s。
2.3 光电复合海缆
待分析的为110 kV单相高压光电复合海底电缆,实测布里渊谱的扫频范围为10.71~11.03 GHz,扫频间隔为10 MHz。入射脉宽为200 ns,波长为1 550 nm,叠加平均次数为213。采用基于伪Voigt模型的谱拟合法计算得到光纤沿线线宽和布里渊频移的均值分别为62.36 MHz和10 873.51 MHz,峰值处布里渊谱的信噪比为37.41 dB。因此,根据式(7)可得单斜坡法工作点选择为10 840 MHz,根据式(9)—式(10)可得双斜坡法工作点分别选择为10 840和10 900 MHz。3种方法算得的光纤沿线布里渊频移如
单斜坡法和双斜坡法算得布里渊频移与谱拟合法的差距分别为0.57和0.47 MHz。考虑到此时谱拟合准确性较高,近似忽略其误差,故双斜坡法的误差为单斜坡法的82.46%。结合
本案例如果使用谱拟合法,则测量海缆复合光纤上所有布里渊谱需要的时间为24.63 s。扫频点数为33,故结合式(12)可知,如果采用单斜坡和双斜坡法则对应的测量时间仅分别为0.75 s和1.49 s。由于温度和应变能有效反映输电线路状态,而根据本文研究结果基于光纤分布式传感能快速测量输电线路中复合光纤的温度和应变,因此能为其状态的快速评估奠定基础。当然,如果希望温度和应变同时测量,则需要再引入一个变量,比如光强,这时候
由
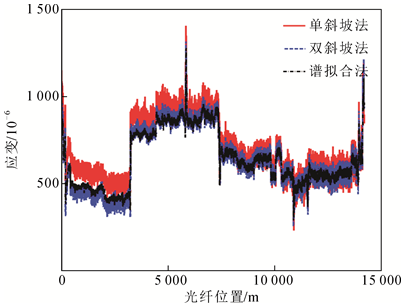
 图8
不同方法算得OPGW复合光纤沿线的应变
Fig.8
Strain along optical fiber composited in OPGW estimated by different methods
图8
不同方法算得OPGW复合光纤沿线的应变
Fig.8
Strain along optical fiber composited in OPGW estimated by different methods
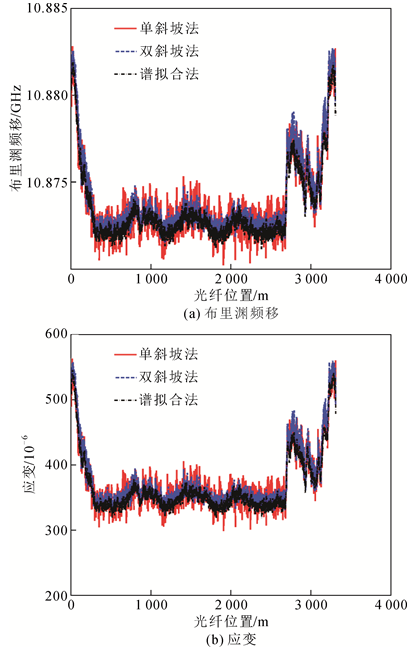
 图9
不同方法算得的海缆复合光纤布里渊频移和应变
Fig.9
Brillouin frequency shift and strain along optical fiber composited in submarine cable estimated by different methods
图9
不同方法算得的海缆复合光纤布里渊频移和应变
Fig.9
Brillouin frequency shift and strain along optical fiber composited in submarine cable estimated by different methods
如果光纤长度仅为100 m同时保持叠加平均次数不变则双斜坡法的准确性可以进一步提高。考虑到频率扫描的切换和稳定时间
在实际应用中,如长距离OPGW等监测对象中,整根光纤往往由多段具有不同布里渊频移的短光纤组成,不同光纤段之间的布里渊频移之差可能较大。如果差别特别大则这种情况不是特别适合于斜坡法,其实也给谱拟合法有效提取布里渊频移带来了一些难度。此时可以通过适当减少入射光脉宽、增加布里渊谱的线宽[32]来提高斜坡法的可用性。
虽然以上案例均针对输电线路,但为了监测电气设备运行状态也可以在其中敷设光纤,本文方法同样也可以监测电气设备光纤沿线的温度和应变,从而为其状态评估奠定基础。
3 影响因素研究
工作点的位置和布里渊谱信噪比会影响双斜坡法的准确性,本章对这2个关键因素的影响进行研究以期能为实际应用时提供参考。
3.1 工作点
本节分别用数值产生布里渊谱和实测布里渊谱分析
采用式(1)的伪Voigt模型数值产生布里渊谱,线宽为40 MHz,
由
实测谱如2.1节所示,

 图10
双斜坡法布里渊频移误差与
图10
双斜坡法布里渊频移误差与
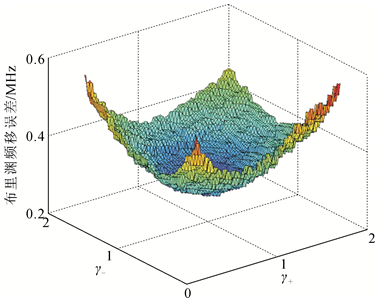
 图11
双斜坡法布里渊频移误差与
图11
双斜坡法布里渊频移误差与
3.2 信噪比
式中:
由
由
4 结论
1)双斜坡法左右2个最佳工作点为光纤沿线布里渊频移的均值加减半个线宽;随着信噪比的增加双斜坡法误差呈指数规律下降。
2)谱拟合法具有最高的准确性,在信噪比较高(不建议小于30 dB)且光纤沿线布里渊频移波动较小(明显小于1个线宽)时,斜坡法和双斜坡法也能达到与谱拟合法相似的准确性,尤其是双斜坡法准确性要高于单斜坡法(前者误差为后者的35.54%~82.46%);谱测量时间可以减少为典型设置下谱拟合法的几十分之一,甚至更小。
基于本文工作有望实现基于布里渊散射的光纤分布式传感的输电线路温度和应变快速测量,甚至传感距离较短时电气设备振动的测量,可为电气设备状态快速评估奠定基础。

 图12
光纤沿线的布里渊频移(仿真)
Fig.12
Brillouin frequency shift along the optical fiber(simulation)
图12
光纤沿线的布里渊频移(仿真)
Fig.12
Brillouin frequency shift along the optical fiber(simulation)

 图13
双斜坡法误差与信噪比的关系(仿真谱)
Fig.13
Change of error in Brillouin frequency shift estimated by double slope-assisted technique with SNR(numerically generated spectra)
图13
双斜坡法误差与信噪比的关系(仿真谱)
Fig.13
Change of error in Brillouin frequency shift estimated by double slope-assisted technique with SNR(numerically generated spectra)

 图14
双斜坡法误差与信噪比的关系(实测谱)
Fig.14
Change of error in Brillouin frequency shift estimated by double slope-assisted technique with SNR(measured spectra)
图14
双斜坡法误差与信噪比的关系(实测谱)
Fig.14
Change of error in Brillouin frequency shift estimated by double slope-assisted technique with SNR(measured spectra)
参考文献
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
[17]
[18]
[19]
[20]
[21]
[22]
[23]
[24]
[25]
[26]
[27]
[28]
[29]
[30]
[31]
[32]


