文章编号: 1000-3673(2021)02-0507-11 中图分类号: TM721 文献标识码: A 学科代码: 470·40
2. 新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司),北京市 海淀区 100192;
3. 国网浙江省电力有限公司湖州供电公司,浙江省 湖州市 313000
2. State Key Laboratory of Control and Operation of Renewable Energy and Storage Systems (China Electric Power Research Institute), Haidian District, Beijing 100192, China;
3. Huzhou Power Supply Company, State Grid Zhejiang Electric Power Company Limited, Huzhou 313000, Zhejiang Province, China
电动汽车(electric vehicle,EV)作为新一代的绿色交通工具,在减少二氧化碳排放、缓解能源危机等方面具有巨大的优势和潜能[1-2]。伴随着具有较强随机性的电动汽车充电负荷的大规模接入,配电网的安全经济运行面临着巨大挑战。相较于慢充负荷,快充电站充电负荷的瞬时功率更大,充电时间和充电地点的选择更加随机,由此导致的配电网线路阻塞、电压越限、网损增加等问题更加突出[3-5],显著提高了电力部门调控的难度。因此,开展针对快充电站充电负荷的建模及相关调控方法的研究十分必要。
电动汽车充电负荷建模是开展相关优化调度方法研究的基础。针对区域内新建快充电站,由于历史充电负荷数据不足,无法基于历史数据开展充电负荷日前预测。对于此类历史充电负荷数据缺失的情况,结合区域历史车辆出行数据模拟用户出行行为,进而获取充电负荷的概率场景是目前主要的研究手段,大部分文献主要从时间和空间两个维度开展相关建模研究[6]。文献[7-8]基于统计学建模的方法得到电动汽车的日行驶里程、起始充电时间和起始荷电状态(state of charge,SOC)等充电行为相关参数的概率分布,再利用蒙特卡洛模拟方法得到一天内电动汽车的充电负荷;文献[9]采用经典排队论方法对充电负荷进行建模,利用泊松分布描述电动汽车到达住宅区的两阶段时间,并得到充电负荷的集聚特性,进而实现充电站内充电设施的优化配置。以上方法均从时间维度着手展开电动汽车充电负荷的建模,但模型较为简单,对充电负荷的时空特性和随机性反映不足。作为一种可移动负荷,电动汽车充电负荷特性与用户出行行为、电池续航能力、交通网络拓扑和流量等因素密切相关,需综合考虑交通网和配电网的耦合影响。为此,文献[10]基于改进的停车生成概率模型建立电动汽车的停车需求时空分布,得到不同区域的电动汽车停车需求;文献[11]将对偶图与描述电动汽车路径选择的马尔科夫链相结合,得到一天中3个典型时段区域内各路段的流量和在不同路段充电站的车辆到达率。然而,上述文献对于电动汽车充电需求的预测仍然采用基于时间维度的方法。文献[12]采用起止点(origin-destination,OD)分析法,通过已有的交通数据在相关软件上反推得到用于模拟车辆行驶路径的OD矩阵,进而基于路径最短原则确定电动汽车的行驶行为,但忽略了路网流量对行驶时间的影响,可能导致得到的出行路径具有很高的时间成本;文献[13]在描述出行类型的马尔科夫链基础上对电动汽车的时空特性进行建模,得到各充电站的充电负荷概率模型,但缺乏对电动汽车在道路上的行为模拟。
另一方面,由于新能源发电既能减少对于传统能源的依赖,又能缓解电网的供电压力,近年来得到广泛利用。为了减少电动汽车充电负荷对配电网的冲击,不少研究探讨了在充电站中引入分布式发电技术支撑电动汽车充电负荷的新形式。如文献[14]在充电站内引入光伏和储能系统,并搭建了以降低购电费用和蓄电池组循环电量为目标的多目标优化调度模型;文献[15]在考虑随机因素对电动公交车充电需求影响的基础上,提出了以充电站运行成本最小为目标的光储充电站日前-日内多时间尺度优化策略。但以上文献研究对象仅涉及含光伏和储能的充电站,未统筹考虑光储充电站接入场景下的配电网优化调度问题。文献[16]在考虑电网约束条件的基础上,建立了以负荷波动最小、可再生能源利用率最大和车主收益最大为目标的多目标优化调度模型,结果表明所提方法可增加可再生能源利用率,改善需求供应不平衡问题,并提高车主收益;文献[17]研究了大规模电动汽车接入配电网后与分布式电源的协调运行调度问题,并提出了一种电动汽车接入主动配电网的多目标优化模型。文献[16]和文献[17]的模型中虽然都考虑了电网运行约束,但未计及电动汽车充电负荷波动的不确定性对配电网产生的影响。文献[18]以路网“均衡模型”规划电动汽车用户出行路径,考虑电动汽车充电的随机性,搭建了耦合交通系统的配电网鲁棒调度模型,但文中未考虑电动汽车充电负荷时序变化对配电网调度的影响。
在此背景下,本文以路网-电力系统的耦合影响为出发点,开展光储快充一体站大规模接入场景下的配电网优化调度问题研究。首先,基于道路交通模型、电动汽车模型及用户出行模型,对区域内快充电站充电负荷进行建模。然后,以随机-鲁棒混合优化为技术手段,建立计及快充负荷、光伏及配电网原有负荷不确定性的配电网日前优化调度模型。最后,通过算例分析验证了所提方法的有效性。
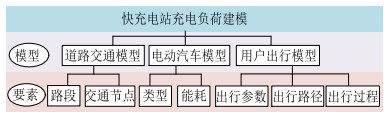
1 快充电站充电负荷建模如前所述,本文以新建光储快充一体站接入配电网的协调优化为应用场景,以历史车辆出行数据模拟电动汽车用户在该区域的出行行为,进而获取充电负荷的随机概率场景。整体建模框架如图 1所示。
|
图 1 电动汽车充电负荷建模框架 Fig. 1 Modelling framework of EV charging loads |
对于道路交通建模,参考经典图论方法,采用表示道路权值的邻接矩阵D描述交通节点与路段之间的关系,矩阵中的元素dij表示对应路段的长度。
| ${\boldsymbol{D}} = \left[ {\begin{array}{*{20}{l}} 0&{{l_{12}}}&{\inf }& \cdots &{\inf } \\ {{l_{21}}}&0&{{l_{23}}}& \cdots &{\inf } \\ {\inf }&{{l_{32}}}&0& \cdots &{\inf } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {\inf }&{\inf }&{\inf }& \cdots &0 \end{array}} \right]$ | (1) |
| $ {d_{ij}} = \left\{ {\begin{array}{*{20}{l}} {{l_{ij}}{\rm{,}}\;\;路段(i,j){\rm{的长度}}}\\ {{\rm{0,}}\;\;\;\;\;\;\;\;\;\;i = j}\\ {{\rm{inf,}}\;\;路段(i,j){\rm{不连通}}} \end{array}} \right.\;\;\;\;\;{\rm{,}}\;i,j \in {N_T}$ | (2) |
式中:lij表示路段(i, j)的长度;inf表示无穷大;NT表示路网中所有交通节点的集合。
1.2 电动汽车模型本文主要考虑私家车和出租车2种类型的电动汽车充电负荷建模。电动汽车充电需求的时间和空间分布特性与其行驶过程中的能耗密切相关,因此本节重点研究其行驶过程中的能耗模型。文献[19]给出了电动汽车内部电动系统的组成,并通过动力学试验得到某型号电动汽车的能耗相关参数,其直流侧有功功率Pdc的计算公式为
| ${P_{{\rm{dc}}}} = \frac{{[\frac{{({P_{\rm{a}}} + {P_{\rm{b}}}v + {P_{\rm{c}}}{v^2} + ma)r}}{{{\eta _{\rm{g}}}{n_{\rm{g}}}}} + {M_{{\rm{CF}}}}]v{n_{\rm{g}}}}}{{{\eta _{\rm{m}}}{P_{{\rm{Fm}}}}{\eta _{{\rm{inv}}}}r}} + {P_{{\rm{aux}}}}$ | (3) |
式中:v为速度,m/s;Pa、Pb、Pc表示阻力参数;m为电动汽车的重量,kg;a表示加速度,m/s2;MCF是经换算后的空载力矩;r为轮胎半径,m;ng和ηg分别表示传输系数比和传输效率;ηm为电动机的效率;PFm为电动机的功率因数;ηinv为逆变器传输效率;Paux表示辅助损耗。
1.3 用户出行模型1)典型出行参数。
电动汽车用户典型出行参数包括出行/返程时间、出发地、目的地、初始SOC、出行路径以及当前的速度、位置和当前SOC。其中,出行/返程时间以及起始出发地、目的地和初始SOC均通过概率分布函数随机抽取生成,出行路径以及当前的速度、位置和SOC的模型获取如下。
2)出行路径规划。
相关研究表明,电动汽车用户出行的时间成本比出行能耗成本更多[20],因此本文在模拟用户行驶行为时,以总出行时间最短为目标。通过路段上电动汽车的平均速度大小计算各路段平均通行时间。路段b的平均通行速度和通行时间为
| ${v_b}(t) = \frac{{\sum\limits_{i = 1}^{{N_b}} {{v_i}(t)} }}{{{N_b}}}$ | (4) |
| ${s_b}(t) = \frac{{{L_b}}}{{{v_b}(t)}}$ | (5) |
式中:vb(t)为路段b中所有电动汽车在时刻t的平均车速;vi(t)为第i辆车在时刻t的速度;Nb为时刻t在路段b上的电动汽车数量;sb(t)为路段b在时刻t的平均通行时间;Lb为路段b的长度。
电动汽车用户在规划出行路径时,还需考虑出行是否有充电需求,而充电需求与电池当前SOC密切相关。假设电动汽车用户在规划出行路径时,SOC与行驶过程能耗呈如下线性关系。
| ${S_{{\rm{OC}}}}_{\rm{d}} = {S_{{\rm{OC}}}}_{\rm{o}} - \frac{{{S_{\rm{d}}}e}}{{{C_{{\rm{EV}}}}}}$ | (6) |
式中:
在模拟电动汽车用户出行路径规划时,若在途中未出现预计剩余电量低于充电阈值的情况,则采用深度搜索算法,得到从出发地到目的地通过时间最短的路径,即
| $\min {\rm{ }}T_{{R_i}}^{o \to d} = \sum\limits_{b \in {N_{\rm{total}}}} {{s_b}(t)} $ | (7) |
式中:o为出发节点;d为交通道路网络中的目的地节点;Ri表示从o到d的第i条路径;Ntotal表示Ri中所有路段的集合。
若在途中出现剩余电量低于充电阈值的情况,则需规划合适的充电站进行充电,此时需考虑用户在充电站内的排队时间和充电时间,排队模型详见文献[21]。同样采用深度搜索算法,选择完成全程所需时间最短的路径和充电站,即
| $\min {\rm{ }}{T_{{\rm{total}}}}{\rm{ = }}T_{{R_i}}^{o \to {C_j}} + T_{\rm{wait}}^{{C_j}} + T_{\rm{charge}}^{{C_j}} + T_{{R_i}}^{{C_j} \to d}$ | (8) |
式中:Cj表示区域内第j号公共充电站;
3)出行过程模拟。
对电动汽车用户的出行路径规划之后,需进一步模拟电动汽车在路上的行驶情况。由大量车辆组成的交通流实际上是一个连续时间、离散事件的复杂系统,因此采用时间、空间和状态变量均定义在离散集上的元胞自动机模型能够较为真实地描述电动汽车在路上的行驶情况。元胞自动机模型如图 2所示(假设车辆从左到右行驶,右上角的数字为车辆当前的速度)。

|
图 2 NS元胞自动机模型 Fig. 2 NS cellular automata model |
根据文献[22],一辆汽车长度为5m,即道路严重拥塞时一辆当量小车所占据的长度,因此取路段上每5m为一个元胞。假设驾驶员的反应(加速或者刹车)时间为1s,作为仿真的时间步长,考虑到汽车在城市道路上行驶的最大速度一般不超过60km/h,因此在一个仿真步长内,汽车不会移动超过3个元胞,即车辆行驶的最大速度vmax为3元胞/s。单位步长内元胞自动机的模拟过程包括慢启动、加速、减速、随机慢化和位置更新等流程,具体行驶规则参见文献[22]。
1.4 快充负荷仿真流程根据前文所介绍的内容,可对区域内快充电站的充电负荷进行建模。采用蒙特卡洛模拟的方法得到区域内各个快充电站一天各统计时段的充电功率。具体仿真流程见附录A。
2 计及快充负荷的配电网随机优化调度 2.1 目标函数如前所述,区域内的时序快充负荷受道路拓扑结构、交通道路流量、电动汽车用户出行时间和充电地点的影响,因此在时间和空间上均表现出较强的随机性。考虑快充负荷不确定性对配电网制定调度方案的影响,本文采用随机优化中的场景分析技术处理快充负荷的不确定性:首先根据上一节对快充负荷的建模仿真,生成大量区域内快充电站充电负荷场景;然后采用场景缩减技术得到原场景的一个近似子集[23],采用K-均值聚类方法对快充负荷场景进行缩减(步骤参见附录B)。
假设配电网内的快充电站、光伏和储能系统等均由配电网运营商投资,因此优化调度的目标函数为最小化配电网运营商的日前运行成本。
| $\begin{array}{*{20}{l}} \min C = \min ({C_{\rm{storage}}} + {C_{\rm{grid}}} + {C_{\rm{loss}}}) = \\ \;\;{\rm{min}} \sum\limits_{t \in {\Omega _t}} {\{ \sum\limits_{m \in {\Omega _{\rm{ess}}}} {{K_{\rm{storage}}}(P_{m,t}^{\rm{dis}}/\eta + P_{m,t}^{\rm{ch}} \cdot \eta )} } + \\ \sum\limits_{s \in {\Omega _s}} {{\omega _s}[K_t^{\rm{price}}P_{s,t}^{\rm{grid}}} + \sum\limits_{i,j \in {\Omega _{\rm{grid}}}} {{K_{\rm{loss}}}I_{ij,s,t}^2{R_{ij}}} ]\} \\ \end{array} $ | (9) |
式中:Cgrid表示配电网购电成本;Closs表示线路网损成本;Cstorage表示储能充放电成本;
1)潮流约束。
配电网交流潮流约束采用基于DistFlow的支路潮流模型表示,具体为
| $\sum\limits_{i:i \to j} {({P_{ij,s,t}} - {R_{ij}}I_{ij,s,t}^2)} - {P_{j,s,t}} = \sum\limits_{k:j \to k} {{P_{jk,s,t}}} $ | (10) |
| $\sum\limits_{i:i \to j} {({Q_{ij,s,t}} - {X_{ij}}I_{ij,s,t}^2)} - {Q_{j,s,t}} = \sum\limits_{k:j \to k} {{Q_{jk,s,t}}} $ | (11) |
| $ U_{j,s,t}^2 = U_{i,s,t}^2 - 2({R_{ij}}{P_{ij,s,t}} + {X_{ij}}{Q_{ij,s,t}}) + (R_{ij}^2 + X_{ij}^2)I_{ij,s,t}^2 $ | (12) |
其中,
| $I_{ij,s,t}^2 = \frac{{P_{ij,s,t}^2 + Q_{ij,s,t}^2}}{{U_{i,s,t}^2}}$ | (13) |
| ${P_{j,s,t}} = P_{j,t}^{\rm{L}} + P_{j,s,t}^{\rm{EV}} + P_{j,t}^{\rm{ch}} - P_{j,t}^{\rm{dis}} - P_{j,t}^{\rm{PV}}$ | (14) |
| ${Q_{j,s,t}} = Q_{j,t}^{\rm{L}} - Q_{j,t}^{\rm{SVC}} - Q_{j,t}^{\rm{ESS}}$ | (15) |
式中:i→j表示节点i为节点j的上游节点;Iij, s, t表示场景s在t时刻从节点i向节点j流出的电流;Ui, s, t和Uj, s, t分别为场景s在t时刻节点i和节点j的电压幅值;Pij, s, t和Qij, s, t分别表示场景s在t时刻从节点i向节点j流出的有功功率和无功功率;Pj, s, t和Qj, s, t为场景s在t时刻节点j净负荷有功功率和无功功率;Rij和Xij表示节点i和节点j间线路的电阻值和电抗值;
基于二阶锥松弛方法,将式(13)转换为旋转二阶锥的形式,并且用线性变量iij, s, t和ui, s, t分别替换式(10)—(13)的平方项
| $\sum\limits_{i:i \to j} {({P_{ij,s,t}} - {R_{ij}}{i_{ij,s,t}})} - {P_{j,s,t}} = \sum\limits_{k:j \to k} {{P_{jk,s,t}}} $ | (16) |
| $\sum\limits_{i:i \to j} {({Q_{ij,s,t}} - {X_{ij}}{i_{ij,s,t}})} - {Q_{j,s,t}} = \sum\limits_{k:j \to k} {{Q_{jk,s,t}}} $ | (17) |
| ${u_{j,s,t}} = {u_{i,s,t}} - 2({R_{ij}}{P_{ij,s,t}} + {X_{ij}}{Q_{ij,s,t}}) + (R_{ij}^2 + X_{ij}^2){i_{ij,s,t}}$ | (18) |
| $\left\| {\begin{array}{*{20}{c}} {2{P_{ij,s,t}}} \\ {2{Q_{ij,s,t}}} \\ {{u_{i,s,t}} - {i_{ij,s,t}}} \end{array}} \right\| \le {u_{i,s,t}} + {i_{ij,s,t}}$ | (19) |
2)节点电压约束。
| ${u_{\min }} \le {u_{i,s,t}} \le {u_{\max }}$ | (20) |
式中umax和umin分别为节点电压上、下限的平方值。
3)支路电流约束。
| $0 \le {i_{ij,s,t}} \le {i_{\max }}$ | (21) |
式中imax是支路电流上限的平方值。
4)储能运行约束。
储能装置在运行过程中需满足的约束为
| $0 \le P_{j,t}^{\rm{dis}} \le {\lambda _{j,t}}S_{j,\max }^{\rm{ess}}$ | (22) |
| $0 \le P_{j,t}^{\rm{ch}} \le (1 - {\lambda _{j,t}})S_{j,\max }^{\rm{ess}}$ | (23) |
| $\sqrt {P{{_{j,t}^{\rm{ch}}}^2} + Q{{_{j,t}^{\rm{ess}}}^2}} \le S_{j,\max }^{\rm{ess}}$ | (24) |
| $\sqrt {P{{_{j,t}^{\rm{dis}}}^2} + Q{{_{j,t}^{\rm{ess}}}^2}} \le S_{j,\max }^{\rm{ess}}$ | (25) |
| $\eta \sum\limits_{t = 1}^{\rm{T}} {(P_{j,t}^{\rm{ch}}\Delta t)} - \frac{1}{\eta }\sum\limits_{t = 1}^{\rm{T}} {(P_{j,t}^{\rm{dis}}\Delta t)} = 0$ | (26) |
| $\begin{array}{*{20}{l}} \delta _{\min }^{\rm{ess}}S_j^{\rm{ess}} \le S_j^{\rm{ess}}(0) + \eta \sum\limits_{t = 1}^{\rm{T}} {(P_{j,t}^{\rm{ch}}\Delta t)} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{\eta }\sum\limits_{t = 1}^{\rm{T}} {(P_{j,t}^{\rm{dis}}\Delta t)} \le \delta _{\max }^{\rm{ess}}S_j^{\rm{ess}} \\ \end{array} $ | (27) |
式中:
5)静止无功补偿装置运行约束。
| $ - Q_{\max }^{\rm{SVC}} \le Q_{j,t}^{\rm{SVC}} \le Q_{\max }^{\rm{SVC}}$ | (28) |
式中
在含光储快充一体站的配电网中,光伏发电和配电网原有负荷在日常运行的过程中也具有明显的不确定性。本文采用文献[24]的箱型不确定集表征光伏出力以及配电网内原有负荷的不确定范围,即
| ${\boldsymbol{V}}:\; = \left\{ {\begin{array}{*{20}{l}} \begin{array}{*{20}{l}} P_{j,t}^{\rm{L}} \in [\hat P_{j,t}^{\rm{L}} - \Delta P_{j,t}^{\rm{L}},\hat P_{j,t}^{\rm{L}} + \Delta P_{j,t}^{\rm{L}}],\forall j,t, \\ \sum\limits_{t = 1}^T {\frac{{|P_{j,t}^{\rm{L}} - \hat P_{j,t}^{\rm{L}}|}}{{\Delta P_{j,t}^{\rm{L}}}}} \le {\mathit{\Gamma} ^{\rm{L}}}; \\ \end{array} \\ \begin{array}{*{20}{l}} P_{j,t}^{\rm{PV}} \in [\hat P_{j,t}^{\rm{PV}} - \Delta P_{j,t}^{\rm{PV}},\hat P_{j,t}^{\rm{PV}} + \Delta P_{j,t}^{\rm{PV}}],\forall j,t, \\ \sum\limits_{t = 1}^T {\frac{{|P_{j,t}^{\rm{PV}} - \hat P_{j,t}^{\rm{PV}}|}}{{\Delta P_{j,t}^{\rm{PV}}}}} \le {\mathit{\Gamma}^{\rm{PV}}} \\ \end{array} \end{array}} \right.$ | (29) |
式中:
在式(29)的基础上,可将式(9)转化为如下的随机-鲁棒混合优化调度模型为
| $\begin{array}{*{20}{l}} \min C = {\rm{min}} \sum\limits_{t \in {\mathit{\Omega} _t}} {[\sum\limits_{m \in {\mathit{\Omega} _{\rm{ess}}}} {{K_{\rm{storage}}}(P_{m,t}^{\rm{dis}}/\eta + P_{m,t}^{\rm{ch}} \cdot \eta )} } + \\ \max \min \sum\limits_{s \in {\mathit{\Omega} _s}} {{\omega _s}(K_t^{\rm{price}}P_{s,t}^{\rm{grid}}} + \sum\limits_{i,j \in {\mathit{\Omega} _{\rm{grid}}}} {{K_{\rm{loss}}}I_{ij,s,t}^2{R_{ij}}} )] \\ \end{array} $ | (30) |
从式(30)可以看出,在考虑光伏出力和负荷功率的不确定集合之后,模型由单阶段变为两阶段。约束条件为式(14)—(28)。为了在下文更方便的阐述该优化模型及求解方法,给出该模型的紧凑形式,即
| $\mathop {\min }\limits_{{\boldsymbol{x}} \in {\boldsymbol{X}}} ({\boldsymbol{c }^{\rm{T}}}{\boldsymbol{x }} + \mathop {\max }\limits_{{\boldsymbol{v }} \in {\boldsymbol{V }}} \mathop {\min }\limits_{{\boldsymbol{y }} \in {\boldsymbol{Y }}} {{\boldsymbol{k }}^{\rm{T}}}{\boldsymbol{y }})$ | (31) |
| $\left\{ \begin{array}{*{20}{l}} {\rm{s}}{\rm{.t}}{\rm{.}} \; \; \; \; \; \; \; \; \; {\boldsymbol{Rx}} \ge {\boldsymbol{r}} \\\; \; \; \; \; \; \; \; \; \left\| {\boldsymbol{Hx}} \right\| \le {\boldsymbol{h}} \\ \; {\boldsymbol{\Delta}} ({\boldsymbol{x}},{\boldsymbol{v}}) = \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{Ey}} = {\boldsymbol{Dx}} + {\boldsymbol{v}}} \\ {{\boldsymbol{Ay}} \ge {\boldsymbol{Cx}} + {\boldsymbol{a}}} \\ {\left\| {\boldsymbol{Gy}} \right\| \le {{\boldsymbol{g}}^{\rm{T}}}{\boldsymbol{y}}} \end{array}} \right. \\ \end{array} \right.$ | (32) |
式中:第一阶段优化变量为
本文所搭建的随机-鲁棒混合优化调度模型目的在于得到各快充负荷典型场景下调度成本期望值最小的方案。其核心思想是将原两阶段问题分解为第一阶段主问题和第二阶段子问题。主问题是在光伏出力和配电网原有负荷的“最恶劣”情况下,得到各场景概率下调度成本期望值最小的储能和SVC调度方案;子问题是在主问题得到的调度方案下,根据设置的不确定参数
本文采用C & CG算法[24]对上述两阶段随机-鲁棒混合优化调度模型进行求解。将原问题分解为主问题和子问题,主问题的具体形式为
| $\left\{ {\begin{array}{*{20}{l}} \begin{array}{*{20}{l}} \mathop {\min }\limits_{{\boldsymbol{x}} \in {\boldsymbol{X}}} {{\boldsymbol{c}}^{\rm{T}}}{\boldsymbol{x}} + {\mathit{\Psi }} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\; \; \; \; \; {\boldsymbol{Rx}} \ge {\boldsymbol{r}} \\ \left\| {\boldsymbol{Hx}} \right\| \le {\boldsymbol{h}} \\ \end{array} \\ \begin{array}{*{20}{l}} \; {\mathit{\Psi }} \ge {{\boldsymbol{k}}^{\rm{T}}}{{\boldsymbol{y}}^l} \\ {\boldsymbol{E}}{{\boldsymbol{y}}^l} = {\boldsymbol{Dx}} + {{\boldsymbol{v}}^l} \\ \end{array} \\ {{\boldsymbol{A}}{{\boldsymbol{y}}^l} \ge {\boldsymbol{C}}{{\boldsymbol{x}}^l} + {\boldsymbol{a}}} \\ {\begin{array}{*{20}{l}} {\left\| {{\boldsymbol{G}}{{\boldsymbol{y}}^l}} \right\| \le {{\boldsymbol{g}}^{\rm{T}}}{{\boldsymbol{y}}^l}} \\\;\;\; {\forall l \le k} \end{array}} \end{array}} \right.$ | (33) |
式中:l为当前的迭代次数;yl为第l次迭代时的变量;vl为第l次迭代后得到的“最恶劣”场景下不确定变量v的取值。
子问题的具体形式为
| $\left\{ {\begin{array}{*{20}{l}} {\mathop {\max }\limits_{\mathit{\boldsymbol{v}} \in \mathit{\boldsymbol{V}}} \mathop {\min }\limits_{\mathit{\boldsymbol{y}} \in \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{v}})} {\mathit{\boldsymbol{k}}^{\rm{T}}}\mathit{\boldsymbol{y}}}\\ {\mathit{\boldsymbol{Ey}} = \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{x}}^*} + \mathit{\boldsymbol{v}}}\\ {\mathit{\boldsymbol{Ay}}\ge\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}^*} + \mathit{\boldsymbol{a}}}\\ {\left\| {\mathit{\boldsymbol{Gy}}} \right\| \le {\mathit{\boldsymbol{g}}^{\rm{T}}}\mathit{\boldsymbol{y}}} \end{array}} \right.$ | (34) |
在给定一组v的情况下,内层min问题变为一个二阶锥规划问题,根据强对偶理论可将其转化为对偶问题的max形式,并与外层max问题结合,得到如下形式:
| $\left\{ {\begin{array}{*{20}{c}} {\mathop {\max }\limits_{v,{\mathit{\boldsymbol{\gamma }}_1},{\mathit{\boldsymbol{\gamma }}_2},{\mathit{\boldsymbol{\omega }}_i},{\mathit{\boldsymbol{\varphi }}_i}} {{(\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{x}}^*} + \mathit{\boldsymbol{v}})}^{\rm{T}}}{\mathit{\boldsymbol{\gamma }}_1} + {{(\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}^*} + \mathit{\boldsymbol{a}})}^{\rm{T}}}{\mathit{\boldsymbol{\gamma }}_2}}\\ {{\rm{s}}.{\rm{t}}.\;\;\;\;{\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{\gamma }}_1} + {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{\gamma }}_2} + \sum\limits_i {({\mathit{\boldsymbol{G}}_i}{\mathit{\boldsymbol{\omega }}_i} + {\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{\varphi }}_i}) = \mathit{\boldsymbol{k}}} }\\ {||{\mathit{\boldsymbol{\omega }}_i}|{|_2} \le {\mathit{\boldsymbol{\varphi }}_i},\forall i = 1,2,...,j}\\ {{\mathit{\boldsymbol{\gamma }}_1},{\mathit{\boldsymbol{\gamma }}_2}\ge0,\mathit{\boldsymbol{v}} \in \mathit{\boldsymbol{V}}} \end{array}} \right.$ | (35) |
式中
根据文献[25]的结论,式(35)取到最大值时,不确定变量v的取值应为式(29)所描述波动区间的边界。对于本文所研究问题,配电网原有负荷取到最大值,且光伏出力取到最小值时,配电网的运行成本更高,更符合“最恶劣”场景的定义,因此可将式(29)改写成如下形式:
| ${\boldsymbol{V}}:\; = \left\{ \begin{array}{*{20}{l}} {\boldsymbol{v}} = {({{\boldsymbol{P}}^{\rm{PV}}},{{\boldsymbol{P}}^{\rm{L}}})^{\rm{T}}}| \\ P_{j,t}^{{\rm{PV}}} = \hat P_{j,t}^{{\rm{PV}}} - B_{j,t}^{{\rm{PV}}}\Delta P_{j,t}^{{\rm{PV}}}, \\ \sum\limits_{t = 1}^{\rm{T}} {B_{j,t}^{{\rm{PV}}} \le {\mathit{\Gamma} ^{{\rm{PV}}}};} \\ P_{j,t}^{\rm{L}} = \hat P_{j,t}^{\rm{L}} + B_{j,t}^{\rm{L}}\Delta P_{j,t}^{\rm{L}}, \\ \sum\limits_{t = 1}^{\rm{T}} {B_{j,t}^{\rm{L}} \le {\mathit{\Gamma} ^{\rm{L}}}} \\ \end{array} \right.$ | (36) |
将式(36)中的不确定变量表达式代入式(35),并引入辅助变量B’可将子问题变换成如下的混合整数二阶锥规划模型:
| $\left\{ {\begin{array}{*{20}{l}} {\mathop {\max }\limits_{\mathit{\boldsymbol{v}},{\mathit{\boldsymbol{\gamma }}_1},{\mathit{\boldsymbol{\gamma }}_2},{\mathit{\boldsymbol{\omega }}_i},{\mathit{\boldsymbol{\varphi }}_i}} {{(\mathit{\boldsymbol{a}} + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^*})}^{\rm{T}}}{\mathit{\boldsymbol{\gamma }}_1} + {{(\mathit{\boldsymbol{\hat v}} + \mathit{\boldsymbol{E}}{\mathit{\boldsymbol{x}}^*})}^{\rm{T}}}{\mathit{\boldsymbol{\gamma }}_2} + \mathit{\Delta }{\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{B'}}}\\ {{\rm{s}}.{\rm{t}}.\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{C}}^{\rm{T}}}{\mathit{\boldsymbol{\gamma }}_1} + {\mathit{\boldsymbol{D}}^{\rm{T}}}{\mathit{\boldsymbol{\gamma }}_2} + \sum\limits_i {(\mathit{\boldsymbol{G}}_i^{\rm{T}}{\mathit{\boldsymbol{\omega }}_i} + {\mathit{\boldsymbol{g}}_i}{\mathit{\boldsymbol{\varphi }}_i})} = \mathit{\boldsymbol{k}}}\\\;\;\;\;\;\;\;\;\;\; {||{\mathit{\boldsymbol{\omega }}_i}|{|_2} \le {\mathit{\boldsymbol{\varphi }}_i},\forall i = 1,2,...,j}\\\;\;\;\;\;\;\;\;\;\; {0 \le \mathit{\boldsymbol{B'}} \le {{\bar \gamma }_2}\mathit{\boldsymbol{B}}}\\\;\;\;\;\;\;\;\;\;\; {{\mathit{\boldsymbol{\gamma }}_2} - {{\mathit{\boldsymbol{\bar \gamma }}}_2}(1 - \mathit{\boldsymbol{B}}) \le \mathit{\boldsymbol{B'}} \le {\mathit{\boldsymbol{\gamma }}_2}}\\\;\;\;\;\;\;\;\;\;\; {\sum\limits_{t = 1}^{\rm{T}} {B_{j,t}^{{\rm{PV}}} \le {\mathit{\Gamma }^{{\rm{PV}}}}} }\\\;\;\;\;\;\;\;\;\;\; {\sum\limits_{t = 1}^{\rm{T}} {B_{j,t}^{\rm{L}} \le {\mathit{\Gamma }^{\rm{L}}}} }\\\;\;\;\;\;\;\;\;\;\; {{\mathit{\boldsymbol{\gamma }}_1},{\mathit{\boldsymbol{\gamma }}_2}\ge0,\mathit{\boldsymbol{v}} \in \mathit{\boldsymbol{V}},\mathit{\boldsymbol{B}} \in (0,1)} \end{array}} \right.$ | (37) |
式中:
经过上述推导和转换,两阶段随机-鲁棒混合优化调度模型最终解耦为主问题式(33)和子问题式(37),随后可用C & CG算法进行求解,流程如下:
1)给定一组v值作为初始的最恶劣场景,设定运行成本下界LB=-∞,上界UB=+∞,迭代次数l=1。
2)根据最恶劣场景vl求解主问题,得到最优解
3)将求得的主问题解代入子问题,得到子问题最优值fl(
4)若UB−LB < ε,其中ε为事先设定的一个足够小的收敛阈度,则表明已得到最优解,停止迭代;否则增加变量yll+1及如下约束。
| $\left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \ge {\mathit{\boldsymbol{k}}^{\rm{T}}}{\mathit{\boldsymbol{y}}^{l + 1}}}\\ {\mathit{\boldsymbol{E}}{\mathit{\boldsymbol{y}}^{l + 1}} = \mathit{\boldsymbol{Dx}} + \mathit{\boldsymbol{v}}_{l + 1}^*}\\ {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{y}}^{l + 1}}\ge\mathit{\boldsymbol{Cx}} + \mathit{\boldsymbol{a}}}\\ {||{\mathit{\boldsymbol{G}}_l}{\mathit{\boldsymbol{y}}^{l + 1}}|| \le \mathit{\boldsymbol{g}}_l^{\rm{T}}{\mathit{\boldsymbol{y}}^{l + 1}}} \end{array}} \right.{\rm{ }}$ | (38) |
令l=l+1,返回步骤2),直至算法收敛。
4 算例 4.1 模型及参数采用13节点的Nguyen–Dupuis网络[20]作为交通系统,该路网中共包含19个路段,其网络拓扑见附录D图D1,道路参数见附录D表D1。充电站分别建在6、7、9、11四个交通节点上,各个站内充电桩数量依次为20、10、20和15,充电桩的快充功率为45kW,快充效率为95%。4个快充电站依次接入3个标准IEEE-33节点配电系统(对应编号1、2、3),路网节点与配电网节点的对应关系见附录D表D2。
假定该区域内共有2500辆私家车和700辆出租车(均为电动汽车,其中出租车包含150辆1类出租车和550辆2类出租车)。私家车和出租车的起始和返程出行概率分布见附录C。车辆类型为Nissan Leaf,电池容量为24kW·h。在为电动汽车规划路径时,e取为0.15kW·h/km[26]。假设车辆起始出行的SOC范围为0.8~0.9,充电需求阈值为0.2~0.3[9],充电SOC上限为0.9。
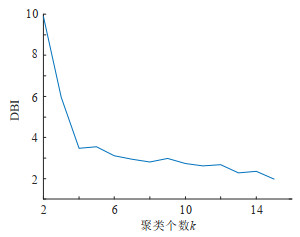
4.2 结果分析 4.2.1 区域内快充负荷建模采用蒙特卡洛仿真方法,随机生成500个区域内各快充电站充电负荷场景,并根据DBI(davies- bouldin index)[27]确定聚类个数k,该指标越小,聚类的效果越优。在不同的聚类个数k下,得到的DBI如图 3所示。
|
图 3 不同聚类个数k下的DBI Fig. 3 DBI under different clustering number k |
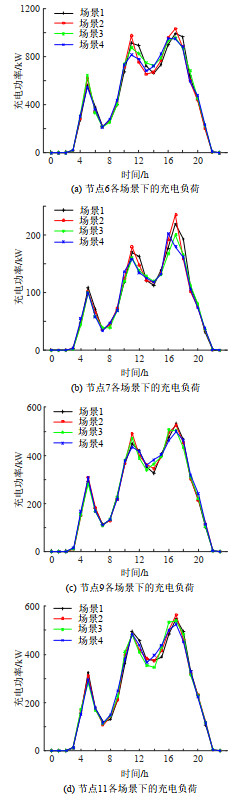
考虑到后续应用到电网优化调度中,聚类个数越多,计算过程越复杂,速度越慢。结合图 3可以看到,在k=4处存在明显的“拐点”,因此选取聚类个数k为4。将500个随机生成的快充负荷场景压缩成4个典型场景,得到的区域内一天中各个快充电站充电负荷情况如图 4所示。
|
图 4 各节点各场景下的充电负荷情况 Fig. 4 Fast charging load in each scenario of each node |
从图 4可以看到,各个场景下,不同快充电站的负荷虽然时序变化情况相似,但是在不同时段数值上存在差异。在凌晨6:00左右出现一个相对较小的充电高峰,这主要是由部分1类出租车在半夜行驶的情况下产生的充电需求所引起的。此外,一天中充电负荷峰值主要集中在中午11:00—12:00和傍晚17:00—18:00。其中,中午11:00—12:00的峰值主要由早上时段出行的2类出租车充电需求及1类出租车的二次充电需求引起,而17:00—18:00点为全天交通出行的高峰期,路段流量变大也将导致电动汽车出行能耗变大,此时私家车、出租车的充电需求叠加,产生充电高峰。以某典型日为例,各时刻进行快充的电动汽车数量如图 5所示。可观察到,电动汽车进行快充的高峰期集中在中午11:00—12:00和傍晚17:00—18:00左右。
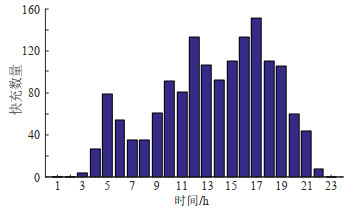
|
图 5 电动汽车快充数量 Fig. 5 Number of fast charging stations of electric vehicles |
各充电站快充负荷在晚上20:00之后逐渐降低,这是由于多数电动汽车用户在夜间选择回家慢充所致。同时,从仿真结果中还可以看出,在快充负荷水平较高的时段,尤其是中午至晚上这段时间,不同场景下的快充负荷区别也相对较大,反映了较大的充电需求与充电地点选择随机性之间的对应关系。
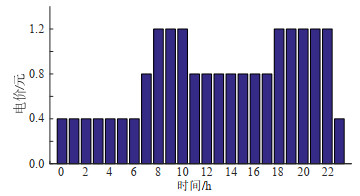
4.2.2 优化调度效果及分析对于快充电站配置光伏和储能电池,配置容量过小不能满足越限时刻的电量需求,容量过大对于充电站功率支撑能力更强,但也需要考虑其经济性。以节点6和节点7所在的1号配电网为例说明,配电网基准功率为10MVA。假设1号配电网的传输容量为3.5MW,根据4.2.1节中得到的快充负荷情况,在节点6和节点7配置的光伏、储能和SVC装置相关参数见附录E表E1。本文考虑光伏出力以及配电网负荷功率的波动偏差分别为预测值的15%和10%,具体预测情况见附录E图E1和图E2。此外,配电网日前交易的分时电价如图 6所示。
|
图 6 配电网交易的分时电价 Fig. 6 Time-of-use electricity prices for distribution network transactions |
1)随机优化效果。
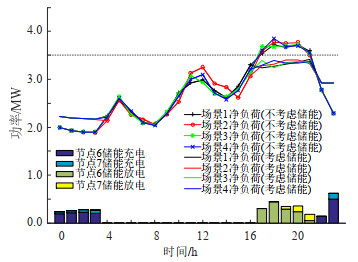
为了说明本文随机-鲁棒混合调度方法的随机优化效果,选择鲁棒优化方案中“最恶劣”的情景,即各时段光伏出力取到下边界,负荷出力取到上边界进行验证。该情景下各场景的配电网净负荷(考虑/不考虑储能)和优化调度得到的储能充放电功率情况如图 7所示。
|
图 7 配电网负荷和储能充放电功率 Fig. 7 Charge and discharge power of energy storage and net load power of distribution network |
图 7虚线表示1号配电网馈线上允许通过的最大有功功率限值。可以看出,白天光伏出力时段,配电网净负荷能够维持在馈线传输功率约束的范围内。但在17:00—21:00的时段内,由于光照强度下降导致光伏出力减少,同时各个场景的快充负荷达到新的高峰,在与配电网原有负荷叠加的情况下,配电网净负荷会出现超出馈线传输功率约束的情况。此时,配电网运营商可通过控制储能系统在该时段内放电,保证配电网净负荷满足馈线传输功率约束的要求,缓解用电负荷高峰对配电网的冲击。为了保证储能电池具备足够剩余容量消纳快充负荷,并满足调度方案的经济性,储能系统在谷电价时段(凌晨0:00—4:00、晚上23:00—0:00)进行充电,以较低的充电成本满足能量需求。此外,为了满足馈线传输功率约束及式(33)所示约束,储能系统将不得不在峰电价时段(22:00—23:00)进行充电。不难发现,储能系统的充放电行为使配电网净负荷曲线趋于平滑。
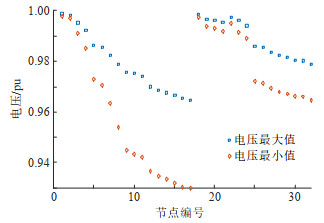
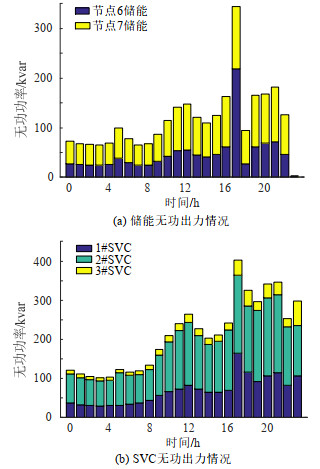
进一步,根据所提出的随机-鲁棒混合优化调度方法,得到的光伏出力和负荷功率“最恶劣”情景下所有场景配电网各节点电压最大值和最小值如图 8所示。从图 8可知,电压水平能够有效维持在电网运行的正常范围内(0.93~1.07pu)。图 9表示储能和SVC的无功出力调度方案。可以看到,具备无功调节功能的储能和SVC在夜间配电网负荷较大的时段无功补偿功率较大,以满足该时段的无功需求,并支撑配电网的电压水平。
|
图 8 配电网节点电压情况 Fig. 8 Node voltage of distribution network |
|
图 9 储能及SVC的无功出力情况 Fig. 9 Reactive power output of energy storage and SVC |
最后,表 1给出了各个随机场景下各项成本的比较。从表中可以看出,因随机-鲁棒混合优化调度的目标为所有场景下的期望成本最小化,所以其调度方案对应的总运行成本介于各随机场景独立优化时的运行成本之间。随机-鲁棒混合优化调度结果的网损、购电和总运行期望成本低于场景2和场景4,但高于场景1和场景3。
|
|
表 1 各场景的成本对比 Table 1 Cost comparison in different scenario |
2)鲁棒优化效果。
为了验证本文所构建随机-鲁棒模型在调度方案保守度上的灵活可调能力,选取3组“不确定调节参数”,分别对调度方案进行比较。3组鲁棒优化调度方案的光伏不确定调节参数
① 方案1。选取
② 方案2。选取
③ 方案3。选取
3组场景对照下的储能充放电成本、网损成本、购电成本以及总运行成本如表 2所示。
|
|
表 2 不同方案下的各项成本对比 Table 2 Cost comparison under different schemes |
从表 2可以看出,当光伏出力和配电网原有负荷不确定性调节参数等于0时,随机-鲁棒混合优化调度模型基于预测值,按最不保守的方案进行优化调度,所以系统内各项期望成本都最低。随着不确定性调节参数的增大,配电网的网损成本、购电成本、储能运行成本和总运行成本也相应地提高。这是因为随着优化调度越多地考虑系统所面临的不确定性,得到的方案越保守,配电网向上级电网购电量和网损均增加,对应的成本也有所增加。同时,考虑配电网线路传输容量限制,储能的作用将不止于削峰填谷,为了满足系统整体运行要求,储能的充放电量和充放电成本也会增加,各方案的储能充放电SOC如图 10所示。
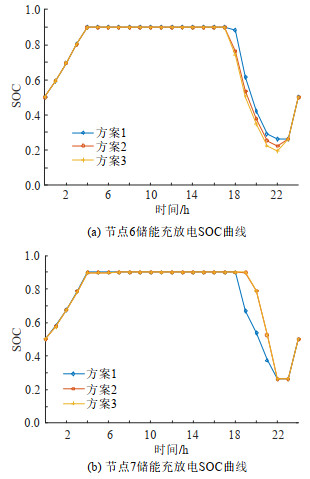
|
图 10 节点6和7的储能充放电SOC曲线 Fig. 10 SOC curve of energy storage of node 6 and node 7 |
图 10(a)中方案2和3的储能放电更快,这是因为17:00的时候,方案2和方案3都取到了配电网负荷功率边界值,而方案1没有取到负荷功率边界值,所以方案1在这个时刻储能对应的放电功率比方案2和3更小,放电速度更慢。在图 10(b)中,3个方案在晚上18:00—22:00峰电价时段储能系统的始末SOC变化量相同,即放电总量是一样的。然而,由于方案2和方案3对应的场景更加恶劣,在19:00—21:00内配电网馈线传输功率会出现越限情况,因此需要集中在该时段内大功率放电。故优化得到的结果是方案1在18:00—21:00 4个峰电价时段放电,而方案2和方案3选择在19:00—21:00 3个峰电价时段放电,保证系统安全运行。
此外,从图 10中还能观察到,方案2和方案3中储能SOC曲线基本类似。在18:00—23:00时段内,图 10(a)中方案3的SOC曲线略低于方案2,意味着储能放电更快。这是由于17:00—19:00方案3的光伏发电预测出力取到最小边界值,在此时段储能的放电功率增加,因此SOC曲线跌落幅度较大。
3)锥强对偶模型验证。
为了验证本文中二阶锥对偶模型的精度,计算得到3个不同方案下主问题的运行成本(不计储能运行成本)和对偶问题的运行成本,如表 3所示。由表 3数据可知,主问题和对偶问题的优化解误差均控制在较小的范围内,可以满足仿真算法中的收敛阈度要求。
|
|
表 3 不同方案下的对偶误差 Table 3 Deviation of dualization under different schemes |
本文提出了一种计及光储快充一体站的配电网随机-鲁棒混合优化调度方法,以某13节点路网-改进的IEEE-33节点配电网的耦合系统为例进行了仿真分析,结果表明:
1)电动汽车快充负荷在时间和空间维度上均表现出一定的不确定性。空间上,区域内各快充电站同一时段接入配电网的充电负荷大小存在差异;在电动汽车充电需求较大的时段,各场景下快充电站充电负荷的区别也较大。时间上,各快充电站的充电负荷时序情况类似,但是不同时段充电负荷大小不同;
2)本文所构建的配电网随机-鲁棒混合优化模型能够通过储能系统的削峰填谷和功率支撑,改善各场景下配电网的潮流分布,并通过不确定调节参数灵活调整调度方案的保守性,提高配电网运行的经济性和鲁棒性。
附录见本刊网络版(http://www.dwjs.com.cn/CN/1000-3673/current.shtml)。
附录A
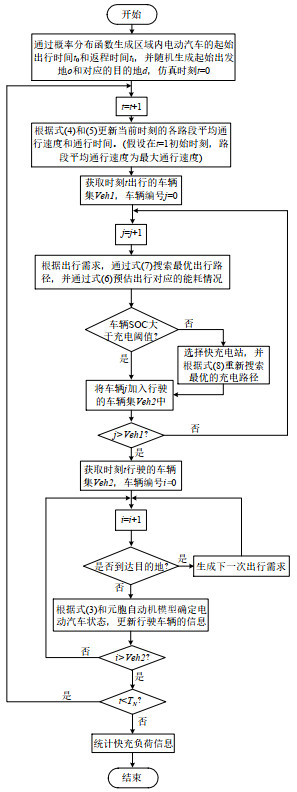
|
图 A1 快充负荷仿真流程图 Fig. A1 Flow chart of fast charging load simulation 注:出行车辆集Veh1为当前时刻准备出行的电动汽车集合,每辆电动汽车的信息包括出行目的地、起始SOC等;行驶车辆集Veh2为当前时刻正在行驶的电动汽车集合,每辆电动汽车的信息包括当前位置、出行路径、驾驶行为,以及当前SOC等;TN表示仿真总步长。 |
K-均值聚类方法对快充负荷场景进行缩减的具体步骤如下:
1)假设快充负荷场景数量为N,聚类数为K,选取K个点c1、c2、…ck(k=1, 2, …, K)作为初始聚类中心,并将以ck为中心的场景集合记为Ck;
2)计算每个场景xi(i=1, 2, …, N)到每个聚类中心ck的欧式距离d(xi, ck)(假设xi={xi1, xi2, ... xin},ci={ci1, ci2, ...cin},d(xi, ck)计算公式如式(B-1)),将其归类到距离最小的集合Ck中;
| $ d({x_i},{c_k}) = \sqrt {{{({x_{i1}} - {c_{k1}})}^2} + {{({x_{i2}} - {c_{k2}})}^2} + \ldots + {{({x_{in}} - {c_{kn}})}^2}} $ | (B-1) |
3)根据聚类后的结果,统计每个集合Ck中的场景数Nk,通过下式重新计算各类的中心,作为新的聚类中心:
| $ {c_k} = \frac{1}{{{N_k}}}\sum\limits_{{x_i} \in {C_k}} {{x_i}} $ | (B-2) |
4)计算第m次迭代的收敛准则函数值:
| $ {I_m} = \sum\limits_{k = 1}^K {\sum\limits_{{x_i} \in {C_k}} {d({x_i},{c_k})} } $ | (B-3) |
5)收敛性判断:如果
场景缩减之后,各场景发生的概率为:
| $ {\rho _k} = \frac{{{N_k}}}{N} $ | (B-4) |
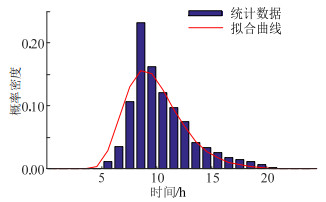
|
图 C1 私家车起始出行时刻分布 Fig. C1 The first traveling time distribution of private cars |
私家车起始出行时刻服从对数正态分布,均值为2.18,标准差为0.30。
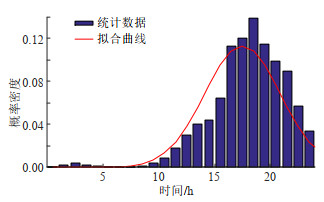
|
图 C2 私家车返程出行时刻分布 Fig. C2 Time distribution of private car return trips |
私家车返程出行时刻服从标准正态分布,均值为16.79,标准差为3.53。
|
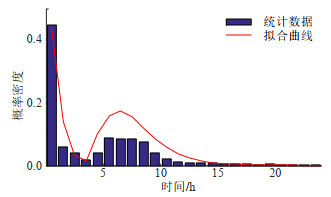
图 C3 出租车起始出行时刻分布 Fig. C3 The first traveling time distribution of taxis |
根据统计数据,出租车起始出行时刻服从分段对数正态分布。假设服从1段分布的出租车为公共出租车(1类),均值为-1.68,标准差为1.41,返程时间为21点至23点;服从2段分布的出租车为私人出租车(2类),均值为1.90,标准差为0.36,返程时间为19点至23点。
附录D
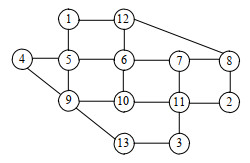
|
图 D1 Nguyen–Dupuis网络 Fig. D1 Nguyen–Dupuis Network |
|
|
表 D1 道路参数 Table D1 Parameters of Roads |
|
|
表 D2 快充站接入配电网对应节点关系表 Table D2 Corresponding nodes for fast charging station accessing distribution network |

|
图 E1 光伏出力情况 Fig. E1 Photovoltaic output |

|
图 E2 配电网原有负荷情况 Fig. E2 Original load of distribution network |
|
|
表 E1 储能和SVC装置参数 Table E1 Parameters of energy storage and SVC |
| [1] |
高赐威, 张亮. 电动汽车充电对电网影响的综述[J]. 电网技术, 2011, 35(2): 127-131. Gao Ciwei, Zhang Liang. A survey of influence of electrics vehicle charging on power grid[J]. Power System Technology, 2011, 35(2): 127-131 (in Chinese). (  0) 0) |
| [2] |
郭建龙, 文福拴. 电动汽车充电对电力系统的影响及其对策[J]. 电力自动化设备, 2015, 35(6): 1-9. Guo Jianlong, Wen Fushuan. Impact of electric vehicle charging on power system and relevant countermeasures[J]. Electric Power Automation Equipment, 2015, 35(6): 1-9 (in Chinese). (  0) 0) |
| [3] |
徐诗鸿, 张宏志, 石栋, 等. 面向智慧城市的快充负荷充电服务费制定策略[J]. 中国电机工程学报, 2020, 40(10): 3187-3201. Xu Shihong, Zhang Hongzhi, Shi Dong, et al. Setting strategy of charging service fee for fast charging load of smart cities[J]. Proceedings of the CSEE, 2020, 40(10): 3187-3201 (in Chinese). (  0) 0) |
| [4] |
侯慧, 徐焘, 柯贤彬, 等. 电动汽车快充对配电网的风险研究[J]. 电力系统保护与控制, 2019, 47(16): 87-93. Hou Hui, Xu Tao, Ke Xianbin, et al. Research on risks of electric vehicle charging to distribution network[J]. Power System Protection and Control, 2019, 47(16): 87-93 (in Chinese). (  0) 0) |
| [5] |
Bosovic A, Music M, Sadovic S.Analysis of the impacts of plug-in electric vehicle charging on the part of a real low voltage distribution network[C]//IEEE Eindhoven PowerTech.Eindhoven: IEEE, 2015: 1-5.
(  0) 0) |
| [6] |
陈丽丹, 张尧, Antonio Figueiredo. 电动汽车充放电负荷预测研究综述[J]. 电力系统自动化, 2019, 43(10): 177-197. Chen Lidan, Zhang Yao, Antonio Figueiredo. Overview of charging and discharging load forcasting for electric vehicles[J]. Automation of Electric Power Systems, 2019, 43(10): 177-197 (in Chinese). (  0) 0) |
| [7] |
Su J, Lie T T, Zamora R. Modelling of large-scale electric vehicles charging demand-a New Zealand case study[J]. Electric Power Systems Research, 2019(167): 171-182. (  0) 0) |
| [8] |
罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011, 35(14): 36-42. Luo Zhuowei, Hu Zechun, Song Yonghua, et al. Study on plug-in electric vehicles charging load calculating[J]. Automation of Electric Power Systems, 2011, 35(14): 36-42 (in Chinese). (  0) 0) |
| [9] |
郑竞宏, 戴梦婷, 张曼, 等. 住宅区式电动汽车充电站负荷集聚特性及其建模[J]. 中国电机工程学报, 2012, 32(22): 32-38. Zheng Jinghong, Dai Mengting, Zhang Man, et al. Load cluster characteristic and modeling of EV charge station in residential district[J]. Proceedings of the CSEE, 2012, 32(22): 32-38 (in Chinese). (  0) 0) |
| [10] |
张洪财, 胡泽春, 宋永华, 等. 考虑时空分布的电动汽车充电负荷预测方法[J]. 电力系统自动化, 2014, 38(1): 13-20. Zhang Hongcai, Hu Zechun, Song Yonghua, et al. A prediction method for electric vehicle charging load considering spatial and temporal distribution[J]. Automation of Electric Power Systems, 2014, 38(1): 13-20 (in Chinese). (  0) 0) |
| [11] |
Arias M B, Kim M, Bae S. Prediction of electric vehicle charging-power demand in realistic urban traffic networks[J]. Applied Energy, 2017(195): 738-753. (  0) 0) |
| [12] |
邵尹池, 穆云飞, 余晓丹, 等. "车-路-网"模式下电动汽车充电负荷时空预测及其对配电网潮流的影响[J]. 中国电机工程学报, 2017, 37(18): 5207-5219. Shao Yinchi, Mu Yunfei, Yu Xiaodan, et al. A spatial-temporal charging load forecast and impact analysis method for distribution network using EVs-traffic-distribution model[J]. Proceedings of the CSEE, 2017, 37(18): 5207-5219 (in Chinese). (  0) 0) |
| [13] |
Tang D, Wang P. Probabilistic modeling of nodal charging demand based on spatial-temporal dynamics of moving electric vehicles[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 627-636. (  0) 0) |
| [14] |
路欣怡, 刘念, 陈征, 等. 电动汽车光伏充电站的多目标优化调度方法[J]. 电工技术学报, 2014, 29(8): 46-56. Lu Xinyi, Liu Nian, Chen Zheng, et al. Multi-objective optimal scheduling for PV-assisted charging station of electric vehicles[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 46-56 (in Chinese). DOI:10.3969/j.issn.1000-6753.2014.08.006 (  0) 0) |
| [15] |
李睿雪, 胡泽春. 电动公交车光储充电站日运行随机优化策略[J]. 电网技术, 2017, 41(12): 3772-3780. Li Ruixue, Hu Zechun. Stochastic optimization strategy for daily operation of electric bus charging station with PV and energy storage[J]. Power System Technology, 2017, 41(12): 3772-3780 (in Chinese). (  0) 0) |
| [16] |
周天沛, 孙伟. 基于微网的电动汽车与电网互动技术[J]. 电力系统自动化, 2018, 42(3): 98-104. Zhou Tianpei, Sun Wei. Electric vehicle-to-grid technology based on microgrid[J]. Automation of Electric Power Systems, 2018, 42(3): 98-104 (in Chinese). (  0) 0) |
| [17] |
肖浩, 裴玮, 孔力. 含大规模电动汽车接入的主动配电网多目标优化调度方法[J]. 电工技术学报, 2017, 32(S2): 179-189. Xiao Hao, Pei Wei, Kong Li. Multi-objective optimization scheduling method for active distribution network with large scale electric vehicles[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 179-189 (in Chinese). (  0) 0) |
| [18] |
Wei W, Mei S W, Wu L, et al. Robust operation of distribution networks coupled with urban transportation infrastructures[J]. IEEE Transactions on Power Systems, 2017, 32(3): 2118-2130. DOI:10.1109/TPWRS.2016.2595523 (  0) 0) |
| [19] |
Hayes J G, Davis K.Simplified electric vehicle powertrain model for range and energy consumption based on EPA coast-down parameters and test validation by Argonne National Lab data on the Nissan Leaf[C]//IEEE Transportation Electrification Conference and Expo (ITEC).Dearborn, MI: IEEE, 2014: 1-6.
(  0) 0) |
| [20] |
He F, Yin Y F, Lawphongpanich S. Network equilibrium models with battery electric vehicles[J]. Transportation Research Part B:Methodological, 2014(67): 306-319. (  0) 0) |
| [21] |
邵尹池, 穆云飞, 林佳颖, 等. "车-站-网"多元需求下的电动汽车快速充电引导策略[J]. 电力系统自动化, 2019, 43(18): 60-68. Shao Yinchi, Mu Yunfei, Lin Jiaying, et al. A fast charging guidance strategy for multiple demands of electric vehicle, fast charging station and distribution network[J]. Automation of Electric Power Systems, 2019, 43(18): 60-68 (in Chinese). (  0) 0) |
| [22] |
赵雪圻, 闫妍, 张峻康, 等. 基于元胞自动机的交通模型分析[J]. 阜阳师范学院学报(自然科学版), 2017, 34(2): 9-14. Zhao Xueyin, Yan Yan, Zhang Junkang, et al. Analysis and application of traffic model based on cellular automaton[J]. Journal of Fuyang Normal University (Natural Science), 2017, 34(2): 9-14 (in Chinese). (  0) 0) |
| [23] |
朱兰, 王吉, 唐陇军, 等. 计及电转气精细化模型的综合能源系统鲁棒随机优化调度[J]. 电网技术, 2019, 43(1): 116-126. Zhu Lan, Wang Ji, Tang Longjun, et al. Robust stochastic optimal dispatching of integrated energy systems considering refined power-to-gas model[J]. Power System Technology, 2019, 43(1): 116-126 (in Chinese). (  0) 0) |
| [24] |
刘一欣, 郭力, 王成山. 微电网两阶段鲁棒优化经济调度方法[J]. 中国电机工程学报, 2018, 38(14): 4013-4022. Liu Yixin, Guo Li, Wang Chengshan. Economic dispatch of microgrid based on two stage robust optimization[J]. Proceedings of the CSEE, 2018, 38(14): 4013-4022 (in Chinese). (  0) 0) |
| [25] |
Bertsimas D, Litvinov E, Sun X A, et al. Adaptive robust optimization for the security constrained unit commitment problem[J]. IEEE Transactions on Power Systems, 2013, 28(1): 52-63. (  0) 0) |
| [26] |
刘洪, 张旭, 刘畅, 等. 考虑充电设施充裕性的电动私家车出行与充电需求时序交互分析[J]. 中国电机工程学报, 2018, 38(18): 5469-5478. Liu Hong, Zhang Xu, Liu Chang, et al. Timing interactive analysis of electric private vehicle traveling and charging demand considering the sufficiency of charging facilities[J]. Proceedings of the CSEE, 2018, 38(18): 5469-5478 (in Chinese). (  0) 0) |
| [27] |
周开乐, 杨善林, 丁帅, 等. 聚类有效性研究综述[J]. 系统工程理论与实践, 2014, 34(9): 2417-2431. Zhou Kaile, Yang Shanlin, Ding Shuai, et al. On cluster validation[J]. Systems Engineering-Theory & Practice, 2014, 34(9): 2417-2431 (in Chinese). (  0) 0) |
 2021, Vol. 45
2021, Vol. 45



 胡代豪(1994),男,硕士研究生,研究方向为电动汽车充电负荷建模及储能在配电网中应用,E-mail:
胡代豪(1994),男,硕士研究生,研究方向为电动汽车充电负荷建模及储能在配电网中应用,E-mail: